문제 링크 : https://www.acmicpc.net/problem/1011

문제

우현이는 어린 시절, 지구 외의 다른 행성에서도 인류들이 살아갈 수 있는 미래가 오리라 믿었다. 그리고 그가 지구라는 세상에 발을 내려 놓은 지 23년이 지난 지금, 세계 최연소 ASNA 우주 비행사가 되어 새로운 세계에 발을 내려 놓는 영광의 순간을 기다리고 있다.

그가 탑승하게 될 우주선은 Alpha Centauri라는 새로운 인류의 보금자리를 개척하기 위한 대규모 생활 유지 시스템을 탑재하고 있기 때문에, 그 크기와 질량이 엄청난 이유로 최신기술력을 총 동원하여 개발한 공간이동 장치를 탑재하였다. 하지만 이 공간이동 장치는 이동 거리를 급격하게 늘릴 경우 기계에 심각한 결함이 발생하는 단점이 있어서, 이전 작동시기에 k광년을 이동하였을 때는 $k-1$ , $k$ 혹은 $k+1$ 광년만을 다시 이동할 수 있다. 예를 들어, 이 장치를 처음 작동시킬 경우 -1 , 0 , 1 광년을 이론상 이동할 수 있으나 사실상 음수 혹은 0 거리만큼의 이동은 의미가 없으므로 1 광년을 이동할 수 있으며, 그 다음에는 0 , 1 , 2 광년을 이동할 수 있는 것이다. ( 여기서 다시 2광년을 이동한다면 다음 시기엔 1, 2, 3 광년을 이동할 수 있다. )

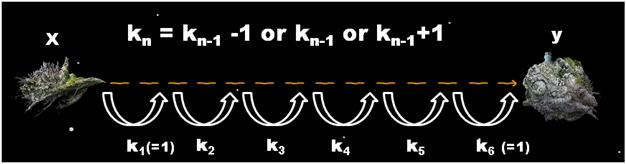
김우현은 공간이동 장치 작동시의 에너지 소모가 크다는 점을 잘 알고 있기 때문에 $x$지점에서 $y$지점을 향해 최소한의 작동 횟수로 이동하려 한다. 하지만 $y$지점에 도착해서도 공간 이동장치의 안전성을 위하여 $y$지점에 도착하기 바로 직전의 이동거리는 반드시 1광년으로 하려 한다.

김우현을 위해 $x$지점부터 정확히 $y$지점으로 이동하는데 필요한 공간 이동 장치 작동 횟수의 최솟값을 구하는 프로그램을 작성하라.

입력

입력의 첫 줄에는 테스트케이스의 개수 $T$가 주어진다. 각각의 테스트 케이스에 대해 현재 위치 $x$ 와 목표 위치 $y$ 가 정수로 주어지며, $x$는 항상 $y$보다 작은 값을 갖는다. $(0 ≤ x < y < 231)$

출력

각 테스트 케이스에 대해 $x$지점으로부터 $y$지점까지 정확히 도달하는데 필요한 최소한의 공간이동 장치 작동 횟수를 출력한다.

풀이

우선 거리 $d$를 구한다. $d = y - x$

그리고 $d$보다 작은 최대의 제곱수 $k^2$를 구한다.

거리가 제곱수일 때에 주목하여 규칙을 살펴보자.

보다시피 제곱수일 때 이동을 살펴보면

$$1,2,3,…,k,…,3,2,1$$

1부터 k까지 1씩 증가하고, 다시 1까지 감소하는 것을 확인할 수 있다.

이때, 이동 거리가 제곱수인 경우 이동 횟수의 일반항을 구할 수 있다.

$$a_{n} = 2n-1$$

거리가 제곱수인 경우를 이용해서 이외의 경우도 구할 수 있다.

$d - k^2<k$ 인 경우, 이동 거리는 거리가 $k^2$일 때 횟수에 1을 더한 값이다.

$d - k^2<2k$ 인 경우, 이동 거리는 거리가 $k^2$일 때 횟수에 2을 더한 값이다.

이를 수식화하면 $2 * k - 1 + [(d - k^2 + k - 1) / k]$ 가 된다.

파이썬 코드로는 2 * k - 1 + (d - k ** 2 + k - 1) // k 가 된다.

소스 코드

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15

n = int(input())

for _ in range(n):
    x, y = map(int, input().split())
    d = y - x
    
    # d보다 작은 최대의 제곱수 k^2
    k = 0
    while k ** 2 <= d:
        k += 1
    k -= 1
    
    result = 2 * k - 1 + (d - k ** 2 + k - 1) // k
    
    print(result)