문제 링크 : https://www.acmicpc.net/problem/14620

문제

2017년 4월 5일 식목일을 맞이한 진아는 나무를 심는 대신 하이테크관 앞 화단에 꽃을 심어 등교할 때 마다 꽃길을 걷고 싶었다.

진아가 가진 꽃의 씨앗은 꽃을 심고나면 정확히 1년후에 꽃이 피므로 진아는 다음해 식목일 부터 꽃길을 걸을 수 있다.

하지만 진아에게는 꽃의 씨앗이 세개밖에 없었으므로 세 개의 꽃이 하나도 죽지 않고 1년후에 꽃잎이 만개하길 원한다.

꽃밭은 N $\times$ N의 격자 모양이고 진아는 씨앗을 (1,1)~(N,N)의 지점 중 한곳에 심을 수 있다. 꽃의 씨앗은 그림 (a)처럼 심어지며 1년 후 꽃이 피면 그림 (b)모양이 된다.

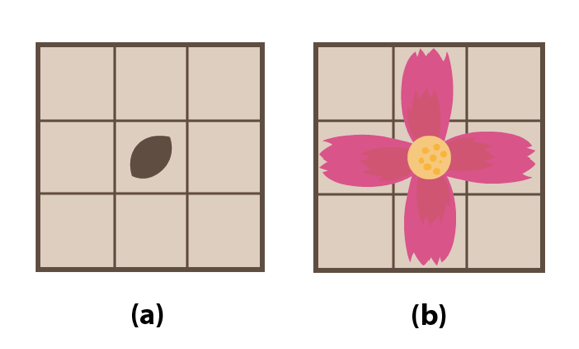
꽃을 심을 때는 주의할 점이있다. 어떤 씨앗이 꽃이 핀 뒤 다른 꽃잎(혹은 꽃술)과 닿게 될 경우 두 꽃 모두 죽어버린다. 또 화단 밖으로 꽃잎이 나가게 된다면 그 꽃은 죽어버리고 만다.

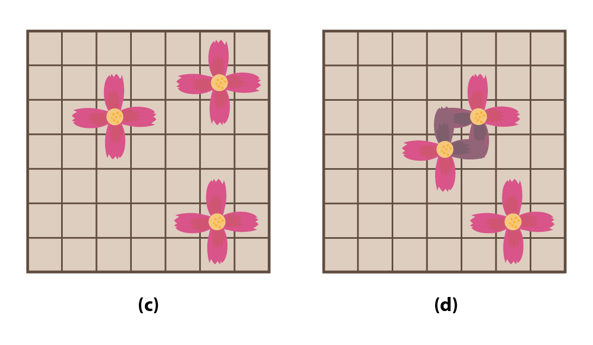
그림(c)는 세 꽃이 정상적으로 핀 모양이고 그림(d)는 두 꽃이 죽어버린 모양이다.

하이테크 앞 화단의 대여 가격은 격자의 한 점마다 다르기 때문에 진아는 서로 다른 세 씨앗을 모두 꽃이 피게하면서 가장 싼 가격에 화단을 대여하고 싶다.

단 화단을 대여할 때는 꽃잎이 핀 모양을 기준으로 대여를 해야하므로 꽃 하나당 5평의 땅을 대여해야만 한다.

돈이 많지 않은 진아를 위하여 진아가 꽃을 심기 위해 필요한 최소비용을 구해주자!

입력

입력의 첫째 줄에 화단의 한 변의 길이 $N (6 \leq N \leq 10)$이 들어온다.

이후 N개의 줄에 N개씩 화단의 지점당 가격$(0 \leq G \leq 200)$이 주어진다.

출력

꽃을 심기 위한 최소 비용을 출력한다.

풀이

꽃이 + 모양으로 생겼기 때문에, 중심점을 잘 생각해야 한다.

다음 그림을 보면서 꽃이 죽는 규칙을 살펴보자.

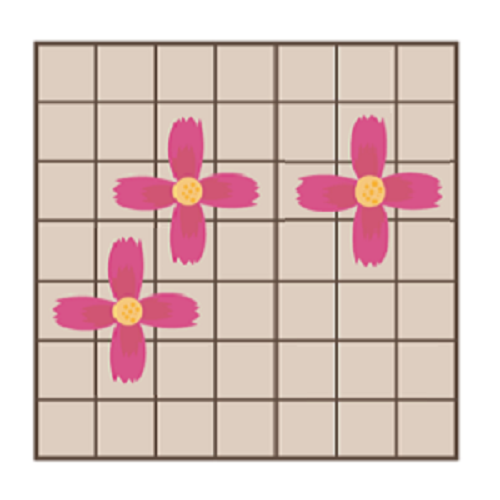
• 중심점의 좌표 $(x,y)$는 $1 \leq x, \space y \leq n-2$ 이다.

• 두 꽃이 서로 겹쳐 죽는 경우는 다음 3가지다.

  • $x_1, x_2$의 차가 $0$인 경우, $y_1, y_2$의 차이가 $3$미만일 때

  • $x_1, x_2$의 차가 $1$인 경우, $y_1, y_2$의 차이가 $2$미만일 때

  • $x_1, x_2$의 차가 $2$인 경우, $y_1, y_2$의 차이가 $1$미만일 때

소스코드

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

import sys
from itertools import combinations

input = sys.stdin.readline
inf = int(2e9)


def is_dead(p1, p2):
    if abs(p1[0] - p2[0]) == 0:
        if abs(p1[1] - p2[1]) < 3:
            return True
    elif abs(p1[0] - p2[0]) == 1:
        if abs(p1[1] - p2[1]) < 2:
            return True
    elif abs(p1[0] - p2[0]) == 2:
        if abs(p1[1] - p2[1]) < 1:
            return True
    return False


def get_cost(p):
    x, y = p
    return cost[y][x] + cost[y-1][x] + cost[y+1][x] + cost[y][x-1] + cost[y][x+1]


def solution(p1, p2, p3):
    if is_dead(p1, p2) or is_dead(p2, p3) or is_dead(p3, p1):
        return inf

    return get_cost(p1) + get_cost(p2) + get_cost(p3)


n = int(input())
cost = [[int(x) for x in input().split()] for _ in range(n)]
pos = [(x, y) for x in range(1, n-1) for y in range(1, n-1)]

result = inf
for p1, p2, p3 in combinations(pos, 3):
    result = min(result, solution(p1, p2, p3))

print(result)