고정 소수점 표현

고정 소수점 방식에서는 정수 부분과 소수 부분을 이진수로 변환한 후 각각 고정된 위치에 표현한다. 아래 그림과 같이 첫번째 비트는 부호를, 그 다음 16비트는 정수를, 우측 15비트는 소수를 나타낸다.

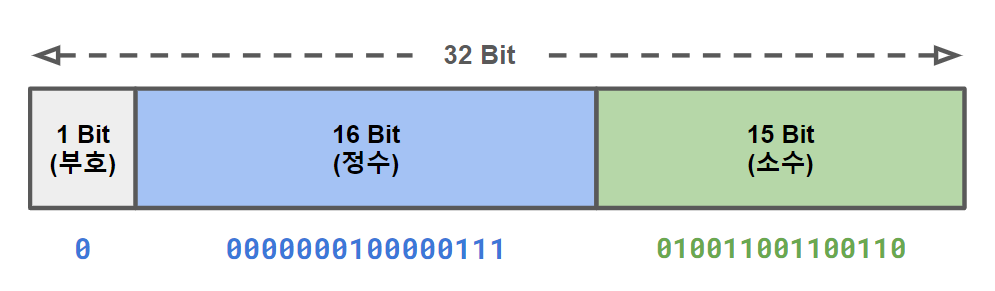
십진 실수를 고정 소수점으로 표현하는 과정은 다음과 같다.

1. 부호(sign)에 양수면 0, 음수면 1을 넣는다.
2. 정수부를 이진화하여, 정수부에 넣는다. 남는 부분은 0으로 채운다.
3. 소수부의 근사치를 이진화하여 소수부에 넣는다. 뒷 부분은 잘라내거나, 남는 부분은 0으로 채운다.

고정 소수점은 부동소수점에 비해 빠르고 간단하다는 장점이 있지만, 정수부로 사용 가능한 비트 수는 정해져 있기 때문에 큰 실수를 표현할 수 없다는 단점이 있다.

부동 소수점 표현

부동소수점 수는 가수(mantissa)와 지수(exponent)로 나누어 표현한다. 아래 그림과 같이 첫번째 비트는 부호를, 그 다음 8비트는 지수를, 우측 23비트는 가수를 나타낸다.

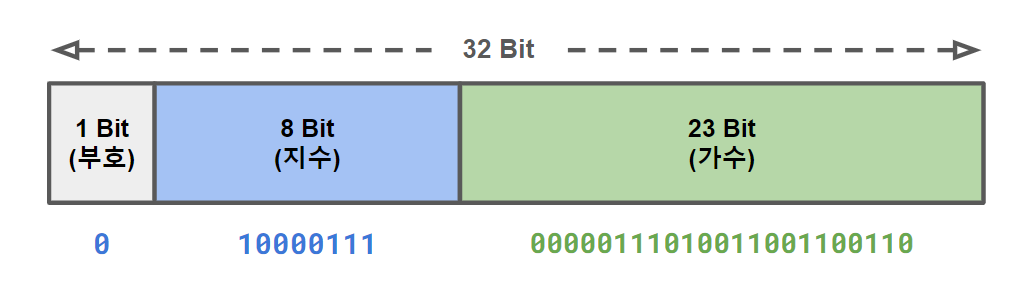
십진 실수를 부동 소수점으로 표현하는 과정은 다음과 같다.

1. 부호(sign)에 양수면 0, 음수면 1을 넣는다.
2. $1.m \times 2^{n}$ 형태로 수를 정규화한다. $m$은 가수, $n$은 지수이다.
3. 정규화된 수의 소수부를 이진화하여 가수에 넣는다. 뒷 부분은 잘라내거나, 0으로 채운다.
4. 지수에 편항(bias) 127을 더해 지수 부분에 담는다. 남는 부분은 0으로 채운다.

부동 소수점은 고정 소수점에 비해 더 큰 실수를 표현할 수 있기에 대부분 부동 소수점을 기본적으로 채택한다.

정규화

부동소수점은 $1.m \times 2^{e-\text{bias}}$ 꼴로 표현되는데, 여기서 정규화란 가수를 $1.m$ 형태로 맞추는 과정이다. 정규화를 통해 동일한 크기의 비트로 더 넓은 범위의 실수를 다룰 수 있다.

1. 실수의 가장 왼쪽에 위치한 1이 가수의 첫 부분에 오도록 위치를 조정한다.
2. 지수 $e$는 가수를 정규화한 결과에 맞게 증가하거나 감소한다.

예를 들어, 10진수 12.75를 부동 소수점으로 변환한다면, 아래와 같다.

1. 12.75를 이진수로 변환하면 $1100.11_2$이다.
2. 정규화하면 $1.10011_2 \times 2^3$이 된다.
3. 여기서 $1.10011_2$는 가수, $3$은 지수가 된다.

정규화를 진행하면 항상 정수부가 1이기 때문에, 1은 굳이 저장하지 않고 소수부만 저장한다. 마찬가지로 $2^{e-\text{bias}}$ 에서 $e$만 가수에 저장한다.

편향 (Bias)

부호 없는 정수 형태로 지수를 표현하기 위해, 실제 지수 값에 특정 값(편향)을 더해 저장한다. 일반적으로 IEEE 754 표준에서는 편향 값으로 $2^{n-1} - 1$을 사용한다. 32비트 단정밀도는 지수 비트수가 8이므로 편향 값은 $127$이다. 계산할 땐 다시 편향 값을 더해 복구한다.

양수와 음수 지수를 모두 다룰 수 있고, 하드웨어 구현이 더 간단해지기 때문에 편향을 이용하여 표현한다. 또한, 0을 정확히 표현할 수 있고, infinity와 NaN을 표현할 수 있다.

부동소수점 오차

부동소수점의 가장 큰 한계 중 하나는 바로 오차이다.

1. 근사 오차 (Rounding Error)
   부동소수점은 유한한 비트로 실수를 표현하기 때문에, 일부 값은 근사치로 표현될 수밖에 없다. 예를 들어, 10진수 0.1은 2진수로 정확히 표현할 수 없기 때문에 근사치로 저장된다.

2. 연산 오차 (Arithmetic Error)
   두 개 이상의 부동소수점 수를 연산할 때, 소수점 아래 비트가 잘리거나 반올림되면서 오차가 발생한다. 특히, 값의 크기 차이가 클수록 오차가 커질 수 있다.

특히, 부동소수점을 == 비교하는 것은 자제하는 것이 옳다.

실수를 더 정확하게 연산하는 방법

정수 연산 치환

항상 소수부가 2자리라면, 100을 곱해 정수로 치환한 뒤, 계산한 후 다시 소수로 변환하는 방법이 있다.

보다 큰 자료형 선택

더 많은 비트를 사용하여, 더욱 정밀도를 높일 수 있다. double 대신 long double, __int128을 사용하면 된다.

분수 클래스 사용

파이썬의 Fraction과 같이, 모든 수를 분수 형태로 표현하여 연산한다면 정확한 실수 연산이 가능하다.

고정 소수점 사용

부동소수점 대신 고정 소수점을 사용하면 일부 환경에서는 오차를 줄일 수 있다. 특히, 값의 범위가 작고 정밀도가 중요한 경우에 적합하다.