본 포스팅은 ‘Mano의 컴퓨터시스템구조’ 교재를 참고했습니다.
조합 회로
조합 회로는 입력과 출력을 가진 논리 게이트의 집합으로 출력의 값은 0과 1들의 조합의 함수이다. 조합 회로와 상반되는 순차 회로는 게이트와 플립플롭 등이 있다.
조합 회로를 설계 절차는 다음과 같다.
- 문제가 제시된다.
- 입력과 출력 변수에 문자 기호를 붙인다.
- 입력과 출력 사이의 관계를 정의하는 진리표를 유도한다.
- 각 출력에 대한 간소화된 부울 함수를 얻는다.
- 논리도를 그린다.
반가산기
반가산기는 비트 두 개를 서로 산술적으로 가산하는 조합 회로이다.
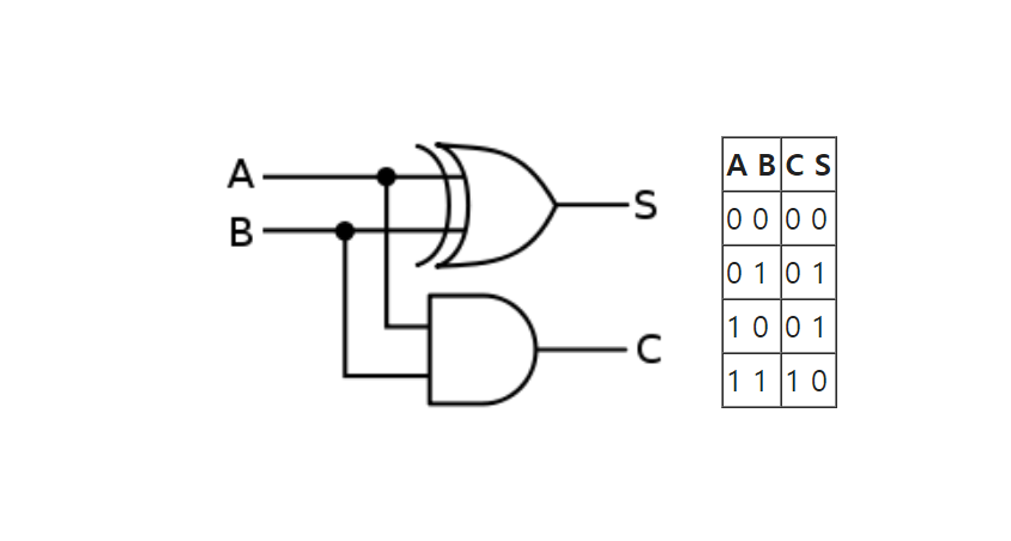
위 그림에서 C는 Carry(캐리, 자리올림)이고, S는 Sum이다.
$A=0, B=1$ 이면 $0+1$ 이므로 $S=1, C=0$이다.
$A=1, B=1$ 이면 $1+1$ 이므로 $S=1, C=1$이다.
A, B 모두 1일 때만 C가 1이 된다. 따라서 C는 $\text{AND}$ 게이트로 구현할 수 있다.
A, B가 서로 다르면 S가 1이 된다. 따라서 S는 $\text{XOR}$ 게이트로 구현할 수 있다.
따라서 반가산기의 논리 표현식은 아래와 같다.
$$ \begin{aligned} S &= x{^\prime}y+xy{^\prime} = x⊕y \ C &= xy \end{aligned} $$
전가산기
전가산기는 비트 두개와 밑의 자리에서 올라오는 캐리까지 고려하여 비트 세 개를 가산하는 조합 회로이다.
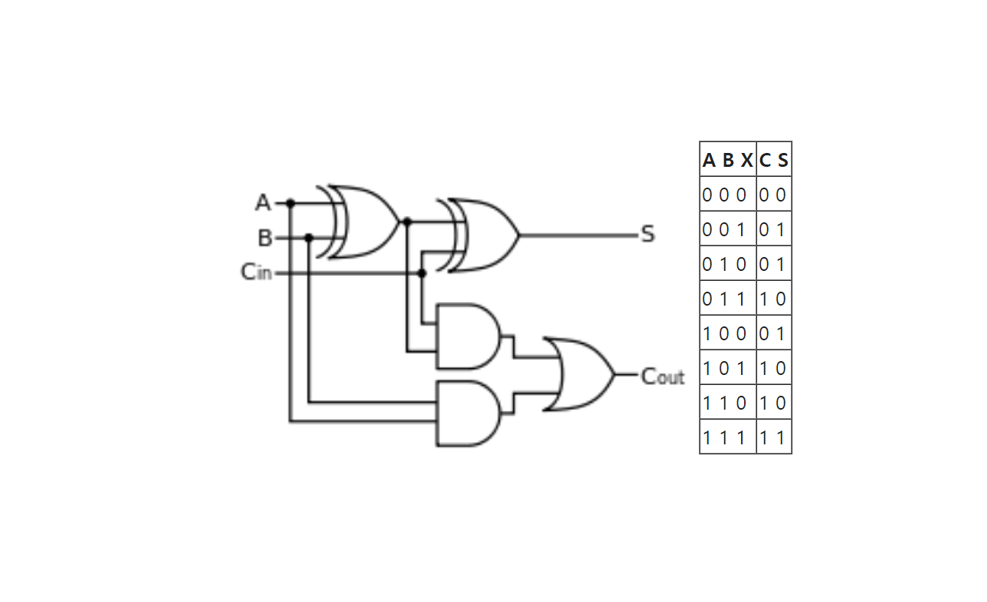
A, B, X에서 1의 개수가 1개 혹은 3개이면 S가 1이 된다.
A, B, X에서 1의 개수가 2개 혹은 3개이면 C가 1이 된다.
전가산기의 논리 표현식은 아래와 같다. 전가산기는 반가산기 두 개와 $\text{OR}$ 게이트로 구현할 수 있다.
$$ \begin{aligned} S &= x⊕y⊕z \ C &= xy+(x⊕y)z \end{aligned} $$
전가산기를 4개 이어붙이면 4비트 덧셈기가 되고, 32개를 이어붙이면 32비트 덧셈기가 된다.
