본 포스팅은 ‘Mano의 컴퓨터시스템구조’ 교재를 참고했습니다.
마이크로 연산
마이크로 연산은 다음 네 가지로 분류된다.
- 레지스터 전송 마이크로 연산
- 산술 마이크로 연산
- 논리 마이크로 연산
- 시프트 마이크로 연산
예를 들어, $R1$과 $R2$의 합을 $R3$에 담으면 아래와 같이 나타낼 수 있다.
$$ R3 \leftarrow R1 + \overline{R2} + 1 $$
$R1$과 $R2$의 차는 아래와 같이 보수를 이용하여 나타낼 수 있다.
$$ R3 \leftarrow R1 + \overline{R2} + 1 $$
이진 가산기
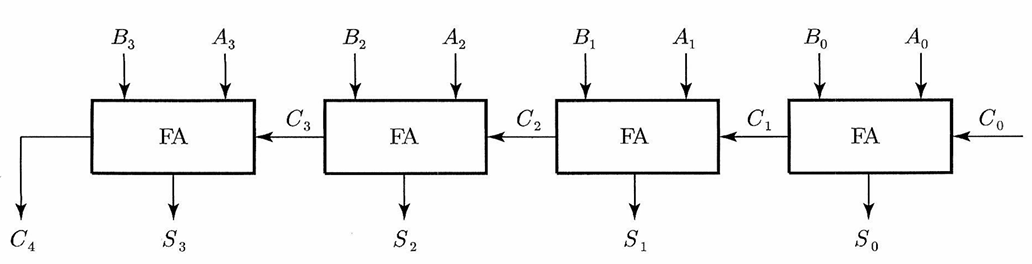
이진 가산기는 산술 마이크로 연산의 대표적인 예시이다. $n$비트 이진 가산기는 $n$개의 전가산기를 직렬로 연결하여 이전 것의 캐리 출력이 다음 것의 캐리로 입력되도록 구성한다.
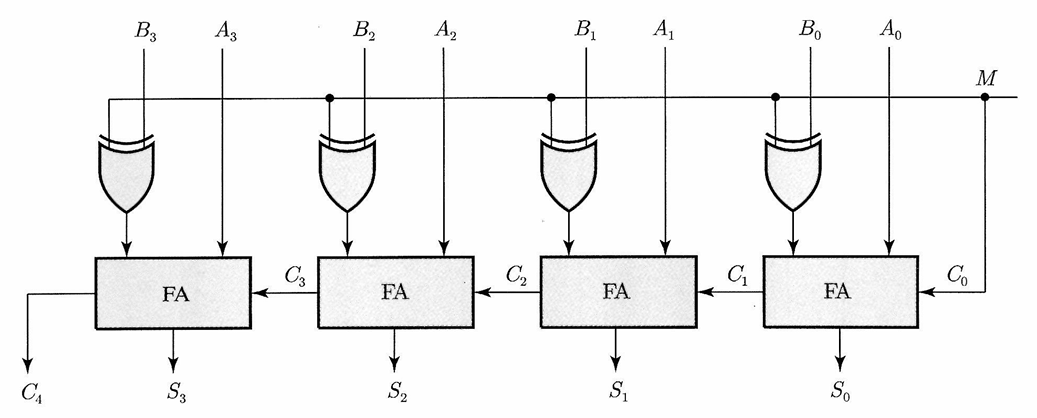
이진 가감산기
이진수의 뺄셈은 2의 보수를 이용하기에, 각 전가산기에 $\text{XOR}$ 게이트를 추가하여 덧셈과 뺄셈을 구현한다. 아래 회로는 $M=0$이면 가산기, $M=1$이면 감산기로 동작한다.
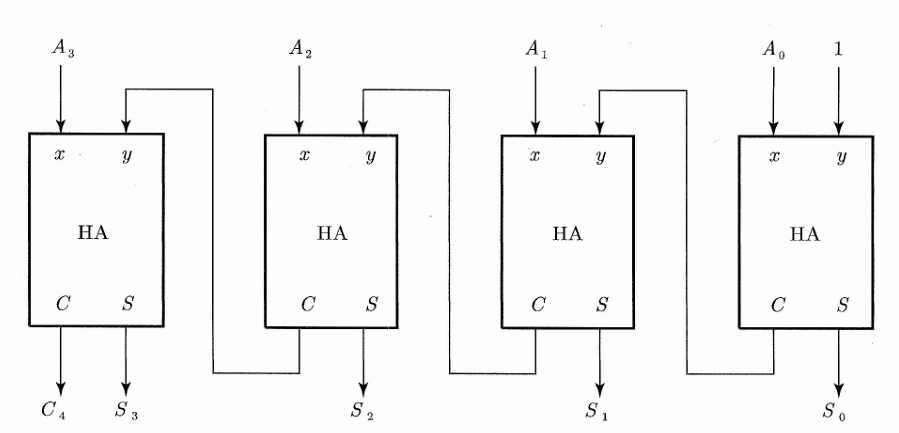
이진 인크리멘터
인크리멘트 마이크로 연산은 레지스터의 값에 1을 더하는 것이다. 카운트 인에이블이 활성화될 때마다 레지스터의 값이 하나씩 증가한다.
논리 마이크로 연산
논리 마이크로 연산은 레지스터에 저장된 비트열에 대한 이진 연산으로 각 비트를 독립된 이진 변수로 간주하고 연산을 수행한다. 예를 들면 아래와 같이 $\text{XOR}$ 연산이 있다.
$$ P: R1 \leftarrow R1 \oplus R2 $$
부울 대수의 $\text{OR}$, $\text{AND}$, 보수 연산과 구별하기 위하여 $\text{OR}$을 $\lor$로, $\text{AND}$를 $\land$로, 1의 보수를 문자 위의 bar로 쓴다. 예를 들면 아래와 같다.
$$ P + Q : R1 \leftarrow R2 + R3, \ R4 \leftarrow R5 \lor R6 $$
| Boolean Function | Microoperation | Name |
|---|---|---|
| $ F_0 = 0 $ | $ F \leftarrow 0 $ | Clear |
| $ F_1 = xy $ | $ F \leftarrow A \land B $ | $\text{AND}$ |
| $ F_2 = xy^\prime $ | $ F \leftarrow A \land \overline{B} $ | |
| $ F_3 = x $ | $ F \leftarrow A $ | Transfer $A$ |
| $ F_4 = x^\prime y $ | $ F \leftarrow \overline{A} \land B $ | |
| $ F_5 = y $ | $ F \leftarrow B $ | Transfer $B$ |
| $ F_6 = x \oplus y $ | $ F \leftarrow A \oplus B $ | $\text{Exclusive-OR}$ |
| $ F_7 = x + y $ | $ F \leftarrow A \lor B $ | $\text{OR}$ |
| $ F_8 = (x + y)^\prime $ | $ F \leftarrow \overline{A \lor B} $ | $\text{NOR}$ |
| $ F_9 = (x \oplus y)^\prime $ | $ F \leftarrow \overline{A \oplus B} $ | $\text{Exclusive-NOR}$ |
| $ F_{10} = y^\prime $ | $ F \leftarrow \overline{B} $ | Complement of $B$ |
| $ F_{11} = x + y^\prime $ | $ F \leftarrow A \lor \overline{B} $ | |
| $ F_{12} = x^\prime $ | $ F \leftarrow \overline{A} $ | Complement of $A$ |
| $ F_{13} = x^\prime + y $ | $ F \leftarrow \overline{A} \lor B $ | |
| $ F_{14} = (xy)^\prime $ | $ F \leftarrow \overline{A \land B} $ | $\text{NAND}$ |
| $ F_{15} = 1 $ | $ F \leftarrow $ all 1’s | Set to all 1’s |
