본 포스팅은 ‘밑바닥부터 시작하는 딥러닝 2’ 교재를 참고했습니다.

신경망의 추론

추론이란 다중 클래스 분류 등의 문제에 답을 구하는 작업이다.

신경망 예시

신경망은 두뇌의 신경세포, 즉 뉴런이 연결된 형태를 모방한 모델이다.

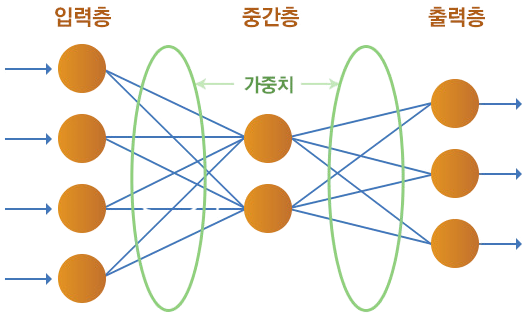
위 신경망의 경우 입력층 4개, 중간층(은닉층) 2개, 출력층 3개로 구성되어 있다.

입력층과 중간층 사이를 보면 인접한 층의 모든 뉴런들이 서로 연결되어 있는데, 이것을 fully connected layer (완전연결계층) 이라고 한다.

가중치와 편향

각 노드 사이에는 가중치가 존재한다. 가중치 값과 뉴런의 값을 곱해 그 합이 다음 뉴런의 입력으로 쓰인다.

또한, 이 때 이전 뉴런의 값에 영향을 받지 않는 정수도 더해지는데, 이 정수를 bias (편향) 이라고 한다.

입력층의 데이터를 $\textbf{x}$, 가중치는 $\textbf{W}$, 편향은 $\textbf{b}$로 나타내면 은닉층의 뉴런 $\textbf{h}$는 다음과 같이 나타낼 수 있다.

$$ \textbf{h} = \textbf{x} \textbf{W} + \textbf{b} \tag{1} $$

Sigmoid 활성화 함수

완전연결계층에 의한 변환은 선형 변환이다. 여기에 비선형 효과를 부여하는 것이 바로 활성화 함수이다. 이를 통해 신경망의 표현력을 높일 수 있다.

가장 대표적인 활성화 함수인 Sigmoid를 알아보자.

xychart-beta
    title "Sigmoid"
    y-axis 0 --> 1
    x-axis [-5, "-4.5", -4, "-3.5", -3, "-2.5", -2, "-1.5", -1, "-0.5", 0, "0.5", 1, "1.5", 2, "2.5", 3, "3.5", 4, "4.5", 5]
    line [0.0066928509242848554, 0.01098694263059318, 0.01798620996209156, 0.02931223075135632, 0.04742587317756678, 0.07585818002124355, 0.11920292202211755, 0.18242552380635635, 0.2689414213699951, 0.3775406687981454, 0.5, 0.6224593312018546, 0.7310585786300049, 0.8175744761936437, 0.8807970779778823, 0.9241418199787566, 0.9525741268224334, 0.9706877692486436, 0.9820137900379085, 0.9890130573694068, 0.9933071490757153]
  

시그모이드 함수는 S자와 유사한 완만한 곡선을 가진다. 식은 아래와 같다.

$$ \sigma(x)=\frac{1}{1+\exp(-x)} \tag{2} $$

이를 파이썬으로 구현하면 다음과 같다.

1
2

def sigmoid(x)： 
    return 1 / (1 + np.exp(-x))

신경망과 순전파의 구현

신경망 추론 과정에서 하는 처리는 순전파(forward propagation)에 해당한다. 말 그대로 입력층에서 출력층으로 향하는 전파이다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

import numpy as np 

# 시그모이드 함수에 의한 변환
class Sigmoid:
    def __init__(self)： 
        self.params = [] 

    def forward(self, x)：
        return 1 / (1 + np.exp(-x))

# 완전연결계층에 의한 변환
class Affine:
    def __init__（self, W, b）： 
        self.params = [W, b]

    def forward(self, x)：
        W, b = self.params 
        return np.matmul(x, W) + b

완전연결계층에 의한 변환은 기하학에서의 Affine 변환에 해당한다.

입력 $\textbf{x}$가 Affine 계층 Sigmoid 계층 Affine 계층을 차례로 거쳐 점수인 $\textbf{s}$를 출력하는 신경망을 만들어 보자.

graph LR
    X==> A[Affine]
    A==> B[Sigmoid]
    B==> C[Affine]
    C==> S[S]
  

이 신경망을 파이썬으로 구현하면 아래와 같다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26

class TwoLayerNet:
    def __init__(self, input_size, hidden_size, output_size)： 
        I, H, O = input_size, hidden_size, output_size

        # 가중치와 편향 초기화
        W1 = np.random.randn(I, H)
        b1 = np.random.randn(H)
        W2 = np.random.randn(H, O)
        b2 = np.random.randn(O)

        # 계층 생성
        self.layers = [
            Affine(W1, b1), 
            Sigmoid(), 
            Affine(W2, b2) 
        ]

        # 모든 가중치를 리스트에 모은다.
        self.params = [] 
        for layer in self.layers:
            self.params += layer.params

    def predict(self, x)：
        for layer in self.layers:
            x = layer.forward(x)
        return x

위에서 구현한 TwoLayerNet 클래스를 이용해 신경망의 추론을 수행해 보자.

1
2
3

x = np.random.randn(10, 2)
model = TwoLayerNet(2, 4, 3) 
s = model.predict(x)

이처럼 계층을 클래스로 만들어두면 신경망을 쉽게 사용할 수 있다.