최적화 함수란?
신경망(neural network)의 학습 목적은 손실 함수(loss function)의 값을 최대한 낮추는 매개변수(parameter)를 찾는 것이다. 이는 곧 매개변수의 최적값을 찾는 문제이며, 이를 최적화 문제(optimization)라고 한다. 최적화 문제를 해결하기 위해 사용하는 도구가 바로 최적화 함수(optimizer)이다.
최적화 함수는 손실 함수의 값을 최소화하는 방향으로 모델의 매개변수를 조정한다. 손실 함수는 예측값(predicted value)과 실제값(true value) 간의 차이를 나타내며, 최적화 함수는 손실을 점진적으로 줄여 모델의 예측 성능을 향상시킨다.
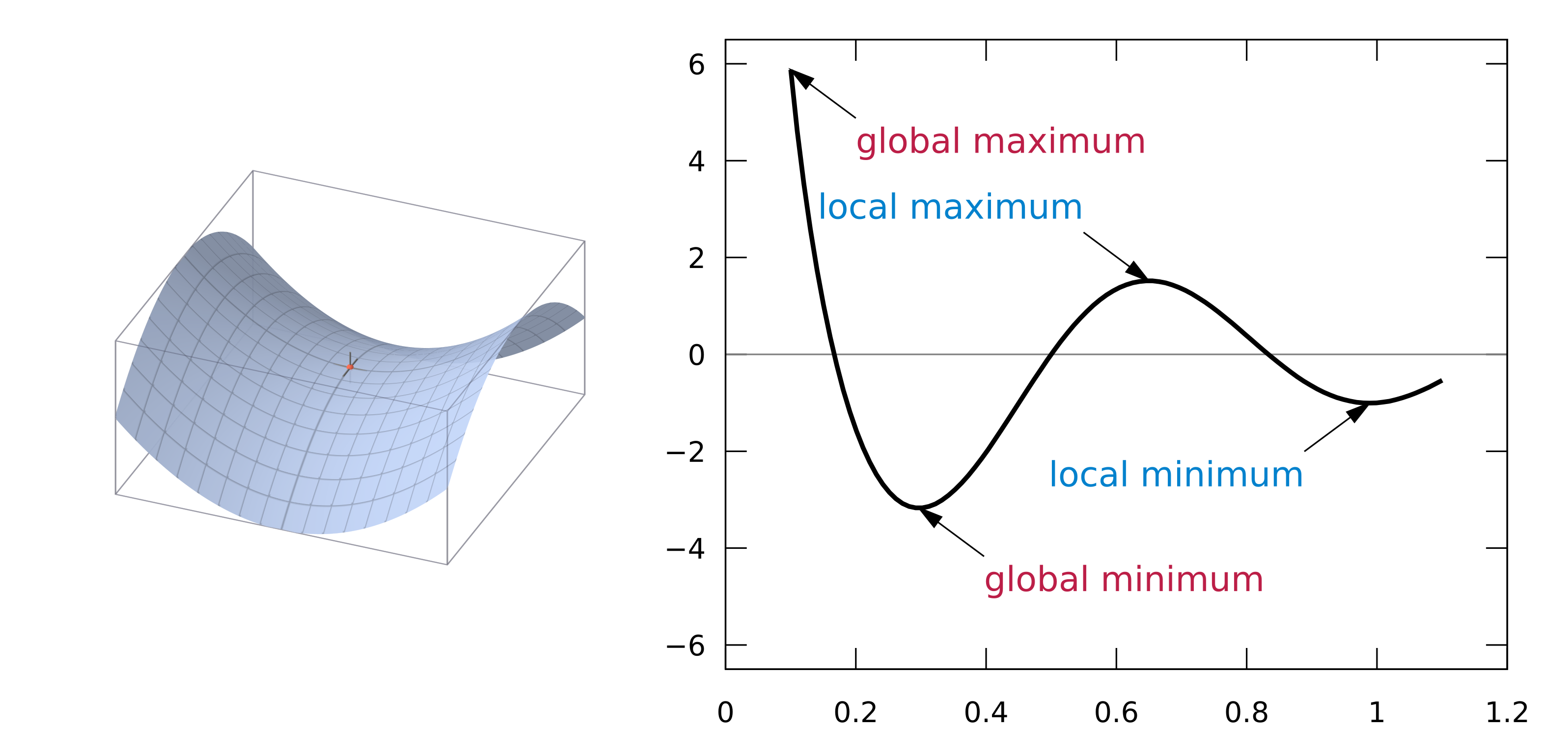
최적화 함수는 기울기(gradient)를 활용하여 손실 함수의 값을 낮추는 방향으로 매개변수를 조정한다. 기울기는 각 지점에서 함수의 값을 줄이는 방향을 나타내는 지표로, 손실 값을 줄이기 위한 업데이트의 핵심 정보를 제공한다. 그러나 딥러닝에서 사용하는 손실 함수는 고차원적이고 복잡한 지형을 가지기 때문에, 기울기가 항상 최적의 방향을 가리킨다고 보장할 수는 없다. 이는 다음과 같은 문제로 이어질 수 있다.
안장점(Saddle Point)
안장점은 특정 방향에서는 극대값처럼 보이고, 다른 방향에서는 극솟값처럼 보이는 지점이다. 이 지점에서는 기울기가 0에 가까워져 학습이 정체될 수 있다.지역 최적해(Local Minimum)
지역 최적해는 특정 구역에서 손실 값이 가장 작은 지점이다. 그러나 이는 전역 최솟값(global minimum)과는 거리가 있을 수 있으며, 최적화 과정이 이 지점에 갇히면 더 나은 해를 찾지 못할 위험이 있다.평탄한 구간(Flat Regions)
손실 함수가 일정하거나 기울기가 매우 작은 평탄한 구간에서는 학습이 느려지거나 멈출 수 있다.
이러한 문제를 극복하고 손실 값을 줄이기 위해, 최적화 함수는 기울기의 정보를 활용해 적절한 방향으로 이동한다. 이러한 접근 방식의 시초가 되는 알고리즘이 바로 경사하강법(Gradient Descent)이다.
Gradient Descent (GD)
경사하강법은 손실 함수의 기울기를 계산하여 손실 값을 줄이는 방향으로 매개변수를 업데이트하는 알고리즘이다.
경사하강법의 기본 수식은 다음과 같다.
$$ \theta_{t+1} = \theta_t - \eta \nabla_{\theta} L(\theta_t) $$
- $ \theta_t $ : 현재 파라미터,
- $ \eta $ : 학습률(learning rate),
- $ \nabla_{\theta} L(\theta_t) $ : 손실 함수의 기울기.
이 수식에서 기울기는 손실 값을 줄이는 방향을 가리킨다. 이를 반복적으로 수행하면 모델의 매개변수가 점진적으로 최적값에 근접한다.
1950s, Stochastic Gradient Descent (SGD)
SGD는 초기의 Batch Gradient Descent의 비효율성을 해결하기 위해 개발되었다. Batch Gradient Descent는 전체 데이터셋을 사용하여 손실 함수의 기울기를 계산하고 파라미터를 업데이트하기 때문에 데이터셋이 클수록 계산 비용이 급격히 증가한다. 이러한 문제를 해결하기 위해 SGD는 데이터의 일부인 샘플이나 미니배치를 사용하여 손실 함수의 기울기를 계산하고 파라미터를 업데이트한다.
SGD의 업데이트 방식은 GD와 거의 같으나, 전체 데이터가 아닌 샘플들을 가지고 gradient 를 구하며 parameter 를 업데이트 해가는 방식이다.
SGD는 전체 데이터셋을 처리하지 않고도 학습을 진행할 수 있어 대규모 데이터 학습에서 계산 비용을 대폭 줄일 수 있다. 또한, 실시간 학습이나 스트리밍 데이터 처리와 같은 환경에서도 효과적으로 사용할 수 있다. 그러나 기울기의 노이즈로 인해 최적점 근처에서 진동(oscillation) 현상이 발생하며, 손실 함수의 평탄한 구간(flat regions)에서는 느리게 수렴한다는 한계가 있다.
PyTorch에서 SGD는 아래와 같이 구현할 수 있다.
| |
1964, Momentum
Momentum은 SGD의 진동 문제를 해결하기 위해 제안되었다. SGD는 현재 기울기만을 기반으로 업데이트를 수행하기 때문에 손실 함수의 지형이 비대칭인 경우 진동이 발생하여 최적점에 도달하는 데 오랜 시간이 걸릴 수 있다. Momentum은 과거 기울기의 이동 평균을 반영하여 더욱 안정적이고 효율적인 학습 경로를 제공한다.
Momentum의 업데이트 방식은 아래와 같다. $$ v_{t+1} = \beta v_t + (1-\beta) \nabla_{\theta_t} L(\theta_t) $$
$$ \theta_{t+1} = \theta_t - \eta_t v_{t+1} $$
- $ v_t $ : 이동 평균(모멘텀 변수),
- $ \beta $ : 모멘텀 계수로, 일반적으로 0.9로 설정된다.
Momentum은 기울기의 이동 평균을 계산하여 진동을 줄이고, 손실 함수가 좁고 깊은 구간에서도 빠르게 수렴할 수 있도록 한다. 그러나 추가적인 하이퍼파라미터 $ \beta $를 적절히 설정해야 한다는 점에서 복잡성이 증가한다.
PyTorch에서 Momentum은 아래와 같이 구현할 수 있다.
| |
1983, Nesterov Accelerated Gradient (NAG)
NAG는 Momentum의 단점을 보완하기 위해 개발되었다. Momentum 방식은 현재 위치에서 기울기를 계산하므로, 최적점 근처에서 오버슈팅(overshooting)이 발생할 가능성이 있다. NAG는 모멘텀에 의해 예측된 미래의 위치에서 기울기를 계산함으로써 이러한 문제를 해결한다.
NAG의 업데이트 방식은 아래와 같다. $$ v_{t+1} = \beta v_t + \nabla_{\theta} L(\theta_t - \eta \beta v_t) $$
$$ \theta_{t+1} = \theta_t - \eta v_{t+1} $$
NAG는 Momentum이 제공하는 이동 방향에 대해 한 단계 더 정교하게 접근하여, 최적점 근처에서의 오버슈팅 문제를 완화한다. 또한, 수렴 속도를 개선하며 최적점 근처에서도 안정적으로 작동한다. 그러나 기울기 계산이 더 복잡해지고 계산 비용이 증가한다는 한계가 있다.
NAG는 PyTorch에서 아래와 같이 구현할 수 있다.
| |
2011, Adagrad
Adagrad는 SGD와 Momentum이 모든 파라미터에 동일한 학습률을 적용한다는 문제를 해결하기 위해 도입되었다. 데이터셋에 드문 특징(sparse feature)이 포함되어 있는 경우, 이러한 방식은 드문 특징을 학습하는 데 비효율적이다. Adagrad는 각 파라미터의 과거 기울기의 제곱합을 기반으로 학습률을 조정하여 이를 해결한다.
Adagrad의 업데이트 방식은 아래와 같다. $$ \theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{G_t + \epsilon}} \nabla_{\theta} L(\theta_t) $$
- $ G_t $ : 과거 기울기의 제곱합,
- $ \epsilon $ : 0으로 나누는 것을 방지하기 위한 작은 값.
Adagrad는 희소 데이터에 대한 학습에서 특히 효과적이며, 각 파라미터에 적응적인 학습률을 적용한다는 점에서 큰 장점이 있다. 그러나 기울기의 제곱합이 점진적으로 증가하면서 학습률이 감소하여 장기 학습에는 적합하지 않다는 한계가 있다.
Adagrad는 PyTorch에서 아래와 같이 구현할 수 있다.
| |
2012, RMSprop
RMSprop은 Adagrad의 단점을 해결하기 위해 제안되었다. Adagrad는 기울기의 제곱합이 점진적으로 증가하여 학습률이 감소하고, 장기 학습에서는 효과가 떨어진다. RMSprop은 기울기의 제곱 이동 평균(Exponentially Weighted Moving Average)을 사용하여 학습률을 조정함으로써 이러한 문제를 해결한다.
RMSprop의 업데이트 방식은 아래와 같다.
$$ E[g^2]_t = \rho E[g^2] _{t-1} + (1-\rho)g_t^2 $$
$$ \theta_{t+1} = \theta _t - \frac{\eta}{\sqrt{E[g^2] _t + \epsilon}} \nabla _{\theta} L(\theta _t) $$
- $ E[g^2]_t $ : 기울기의 제곱 이동 평균,
- $ \rho $ : 지수 이동 평균의 가중치 계수로, 일반적으로 0.9로 설정된다,
- $ \epsilon $ : 0으로 나누는 것을 방지하기 위한 작은 값.
RMSprop은 Adagrad와 달리 이동 평균을 사용하여 학습률 감소 문제를 해결하고, 일정한 학습률을 유지하며 안정적으로 작동한다. 특히 RNN(Recurrent Neural Network)과 같은 모델에서 효과적으로 사용된다.
RMSprop은 PyTorch에서 아래와 같이 구현할 수 있다.
| |
2014, Adam
Adam은 Momentum과 RMSprop의 장점을 결합하여 더욱 효율적이고 안정적인 학습을 제공하기 위해 제안되었다. Adam은 1차 모멘텀(기울기의 이동 평균)과 2차 모멘텀(기울기의 제곱 이동 평균)을 모두 사용하여 학습률을 조정한다.
Adam의 업데이트 방식은 아래와 같다.
$$ m_t = \beta_1 m_{t-1} + (1 - \beta_1)g_t $$
$$ v_t = \beta_2 v_{t-1} + (1 - \beta_2)g_t^2 $$
$$ \hat{m}_t = \frac{m_t}{1-\beta_1^t}, \quad \hat{v}_t = \frac{v_t}{1-\beta_2^t} $$
$$ \theta_{t+1} = \theta_t - \frac{\eta}{\sqrt{\hat{v}_t} + \epsilon} \hat{m}_t $$
- $ m_t $ : 기울기의 1차 모멘텀(평균),
- $ v_t $ : 기울기의 2차 모멘텀(분산),
- $ \hat{m}_t $, $ \hat{v}_t $ : 편향 보정된 모멘텀.
Adam은 빠르고 안정적인 수렴을 제공하며, 대부분의 딥러닝 모델에서 기본 최적화 알고리즘으로 사용된다. 학습률의 조정이 자동으로 이루어져 하이퍼파라미터 설정의 복잡성이 감소하는 장점이 있다. 그러나 과적합 가능성이 높아질 수 있으며, 일반화 성능이 저하될 위험이 있다.
Adam은 PyTorch에서 아래와 같이 구현할 수 있다.
| |
2017, AdamW
AdamW는 Adam의 일반화 성능 문제를 해결하기 위해 제안되었다. Adam은 L2 정규화를 사용하는 방식이 가중치 감쇠(weight decay)와 동일하지 않다는 문제가 있었고, 이는 과적합 위험을 증가시켰다. AdamW는 가중치 감쇠를 명시적으로 적용하여 이러한 문제를 해결하였다.
AdamW의 업데이트 방식은 아래와 같다. $$ \theta_{t+1} = \theta_t - \eta (\hat{m}_t / \sqrt{\hat{v}_t} + \epsilon + \lambda \theta_t) $$
- $ \lambda $ : 가중치 감쇠(weight decay) 계수.
AdamW는 과적합을 줄이고 일반화 성능을 향상시키는 데 효과적이다. 특히 딥러닝 연구와 최신 모델 개발에서 기본 최적화 알고리즘으로 널리 사용되고 있다.
AdamW는 PyTorch에서 아래와 같이 구현할 수 있다.
| |
