정칙화(Regularization)
머신러닝과 딥러닝 모델을 학습시킬 때, 오버피팅은 모델이 훈련 데이터에 지나치게 적합되어 새로운 데이터에 대한 예측 성능이 저하되는 오버피팅(overfitting) 문제는 흔히 접해보았을 것이다. 이러한 문제를 해결하기 위해 사용되는 기술이 바로 정칙화(Regularization)이다.
정칙화는 모델이 암기(Memorization)가 아니라 일반화(Generalization)할 수 있도록 손실 함수에 규제(Penalty)를 가하는 방식이다.
정칙화를 적용하면 학습 데이터들이 갖고 있는 작은 차이점에 대해 덜 민감해져 모델의 분산 값이 낮아진다. 그러므로 정칙화는 모델이 데이터를 학습할 때 의존하는 특징의 수를 줄임으로써 모델의 추론 능 력을 개선한다.
오버피팅과 일반화
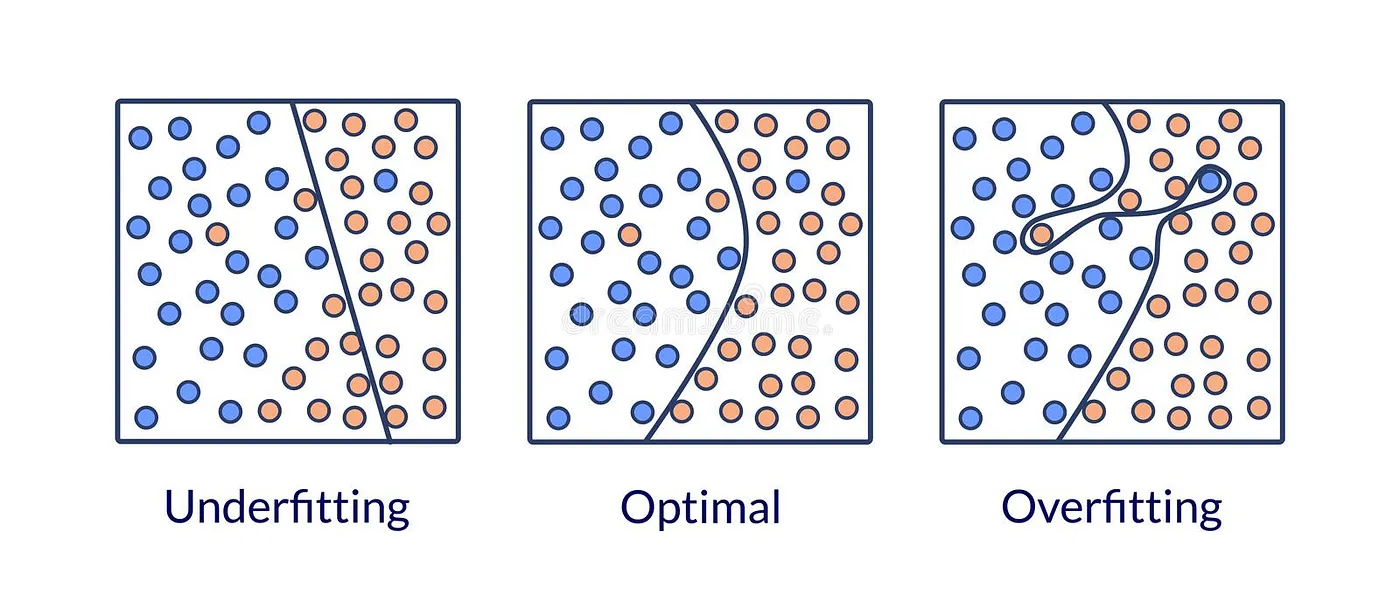
오버피팅은 모델이 훈련 데이터의 노이즈나 특정 패턴을 학습하여, 실제 데이터의 일반적인 패턴을 파악하지 못할 때 발생한다. 이로 인해 모델은 훈련 데이터에서는 높은 성능을 보이지만, 새로운 데이터에서는 성능이 급격히 떨어진다. 반면, 일반화는 모델이 새로운 데이터에서도 정확한 예측을 수행할 수 있는 능력을 의미한다.
즉, 모델이 데이터의 일반적인 패턴을 학습하여 노이즈에 의존하지 않고, 다양한 데이터에 대해 일관된 성능을 유지하는 것이다.
정칙화의 종류
L1 정칙화
L1 정칙화는 라쏘 정칙화(Lasso Regularization)라고도 불리며, 가중치의 절댓값 합을 손실 함수에 추가하여 오버피팅을 방지한다.
이 방식은 모델이 불필요한 피처의 가중치를 0으로 수렴시키는 특징이 있어, 자동으로 특징 선택(feature selection)의 효과를 제공한다. 그러나 L1 정칙화는 하이퍼파라미터인 규제 강도(lambda)를 적절히 조절해야 하며, 과도한 규제는 정보의 손실을 초래할 수 있다. 주로 선형 회귀 모델에서 활용되며, 계산 복잡도가 다소 높을 수 있다는 단점이 있다.
$$ \text{Loss}\text{L1} = \text{Loss}{\text{original}} + \lambda \sum_{i=1}^{n} |w_i| $$
- $ \text{Loss}_{L1} $: L1 정칙화가 적용된 전체 손실 함수
- $ \text{Loss}_{\text{original}} $: 원래의 손실 함수 (ex. 평균 제곱 오차)
- $ \lambda $: 규제 강도 하이퍼파라미터
- $ w_i $: 각 가중치 파라미터
- $ n $: 가중치의 총 개수
L2 정칙화
L2 정칙화는 릿지 정칙화(Ridge Regularization)라고도 하며, 가중치 제곱의 합을 손실 함수에 추가하여 오버피팅을 방지한다.
L2 정칙화는 가중치를 0에 가깝게 유지하므로, 모델의 가중치가 균일하게 분포되도록 도와준다. 이는 모델의 복잡도를 조정하여 일반화 성능을 향상시키는 데 기여한다. L1 정칙화와 달리, L2 정칙화는 모든 가중치를 조금씩 줄이는 경향이 있어, 희소성을 제공하지 않는다. 주로 심층 신경망 모델에서 많이 사용되며, 하이퍼파라미터 조정이 필요하다.
$$ \text{Loss}\text{L2} = \text{Loss}{\text{original}} + \lambda \sum_{i=1}^{n} w_i^2 $$
- $ \text{Loss}_{L2} $: L2 정칙화가 적용된 전체 손실 함수
가중치 감쇠
가중치 감쇠는 L2 정칙화와 유사하게, 손실 함수에 규제 항을 추가하여 모델의 가중치를 작게 유지하는 기법이다.
딥러닝 라이브러리에서는 종종 최적화 함수에 weight_decay 파라미터로 구현되며, L2 정칙화와 동일한 효과를 가진다. 가중치 감쇠는 모델의 일반화 성능을 향상시키기 위해 사용되며, 다른 정칙화 기법과 함께 적용할 때 더욱 효과적일 수 있다.
| |
엘라스틱 넷
엘라스틱 넷(Elastic-Net)은 L1 정칙화와 L2 정칙화를 결합한 방식으로, 두 정칙화의 장점을 동시에 활용한다.
이는 모델이 희소성과 작은 가중치의 균형을 맞추도록 도와주며, 특히 피처의 수가 샘플의 수보다 많을 때 유의미한 성능 향상을 제공한다. 혼합 비율을 조절하여 두 정칙화의 영향을 조절할 수 있으나, 새로운 하이퍼파라미터가 추가되므로 튜닝이 필요하다.
$$ \text{Loss}\text{ElasticNet} = \text{Loss}{\text{original}} + \lambda_1 \sum_{i=1}^{n} |w_i| + \lambda_2 \sum_{i=1}^{n} w_i^2 $$
- $ \lambda_1 $: L1 정칙화의 규제 강도
- $ \lambda_2 $: L2 정칙화의 규제 강도
드롭아웃
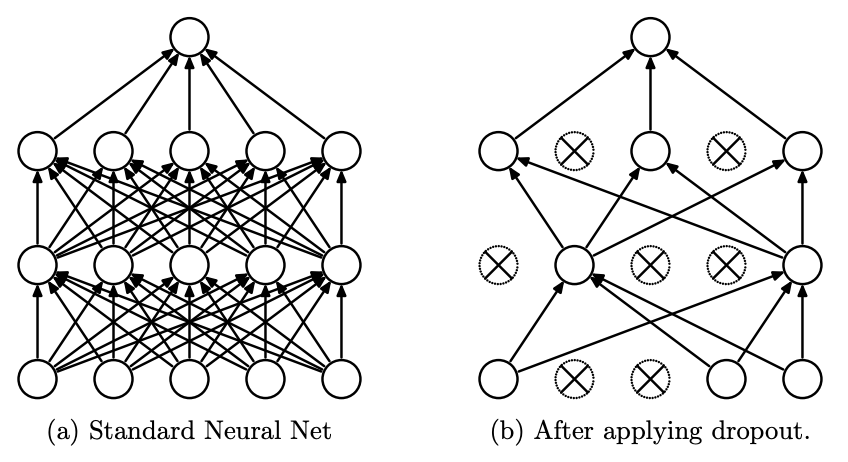
드롭아웃(Dropout)은 신경망의 훈련 과정에서 일부 노드를 임의로 제거하거나 0으로 설정하여 오버피팅을 방지하는 기법이다.
이는 노드 간의 동조화(co-adaptation)를 억제하여 모델이 특정 노드에 지나치게 의존하지 않도록 한다. 드롭아웃은 모델의 일반화 성능을 향상시키는 동시에 모델 평균화 효과를 제공하지만, 충분한 데이터와 깊은 모델에 적용할 때 더욱 효과적이다. 배치 정규화와 함께 사용할 때는 신중하게 조합해야 한다.
$$ y = \begin{cases} 0 & \text{with probability } p \ \frac{y}{1-p} & \text{with probability } 1-p \end{cases} $$
- $ y $: 뉴런의 출력값
- $ p $: 뉴런을 제거할 확률 (드롭아웃 비율)
- $ 1-p $: 뉴런을 유지할 확률
- 출력값을 $ \frac{1}{1-p} $로 스케일링하여 훈련 시와 추론 시의 활성화 분포를 일치
그레이디언트 클리핑
그레이디언트 클리핑(Gradient Clipping)은 모델 학습 시 기울기가 너무 커지는 현상을 방지하기 위해 사용되는 기법이다.
이는 기울기의 크기를 특정 임곗값으로 제한하여, 학습 과정에서 발생할 수 있는 기울기 폭주 문제를 해결한다. 주로 순환 신경망(RNN)이나 LSTM 모델에서 활용되며, 학습률을 조절하는 효과와 유사한 역할을 한다. 그레이디언트 클리핑은 하이퍼파라미터인 최대 임곗값을 신중하게 설정해야 하며, 이를 통해 모델의 안정적인 학습을 도모할 수 있다.
$$ \text{if } ||g||_2 > r, \quad g \leftarrow \frac{g}{||g||_2} \times r $$
- $ g $: 기울기 벡터
- $ ||g||_2 $: 기울기 벡터의 L2 노름
- $ r $: 설정한 임계값 (threshold)
- 기울기의 방향은 유지하면서 크기를 $ r $로 제한
