Featured image of post 순환 신경망(RNN)과 장단기 메모리(LSTM)
파이토치 트랜스포머를 활용한 자연어 처리와 컴퓨터 비전 심층학습

순환 신경망(RNN)과 장단기 메모리(LSTM)

순환 신경망(RNN)과 장단기 메모리(LSTM)의 원리와 구조에 대하여

순환 신경망

순환 신경망(Recurrent Neural Network, RNN)은 시퀀스(Sequence) 데이터를 처리하기 위해 개발된 인공 신경망이다. 일반적인 신경망은 입력과 출력이 독립적이지만, RNN은 각 시점의 데이터가 이전 시점의 데이터에 영향을 받는 구조를 가지고 있어 자연어 처리(NLP), 시계열 분석, 음성 인식 등에 활용된다.

RNN

자연어 데이터와 RNN

자연어 데이터 또한 연속적인 데이터의 일종이다. 문장에서 단어들은 순서대로 등장하며, 이전 단어들이 현재 단어의 의미 형성에 영향을 준다. 자연어는 이전 단어들과의 관계 속에서 문맥을 형성하며, RNN은 이러한 특성을 잘 반영할 수 있도록 설계된 신경망이다.

RNN의 동작 원리

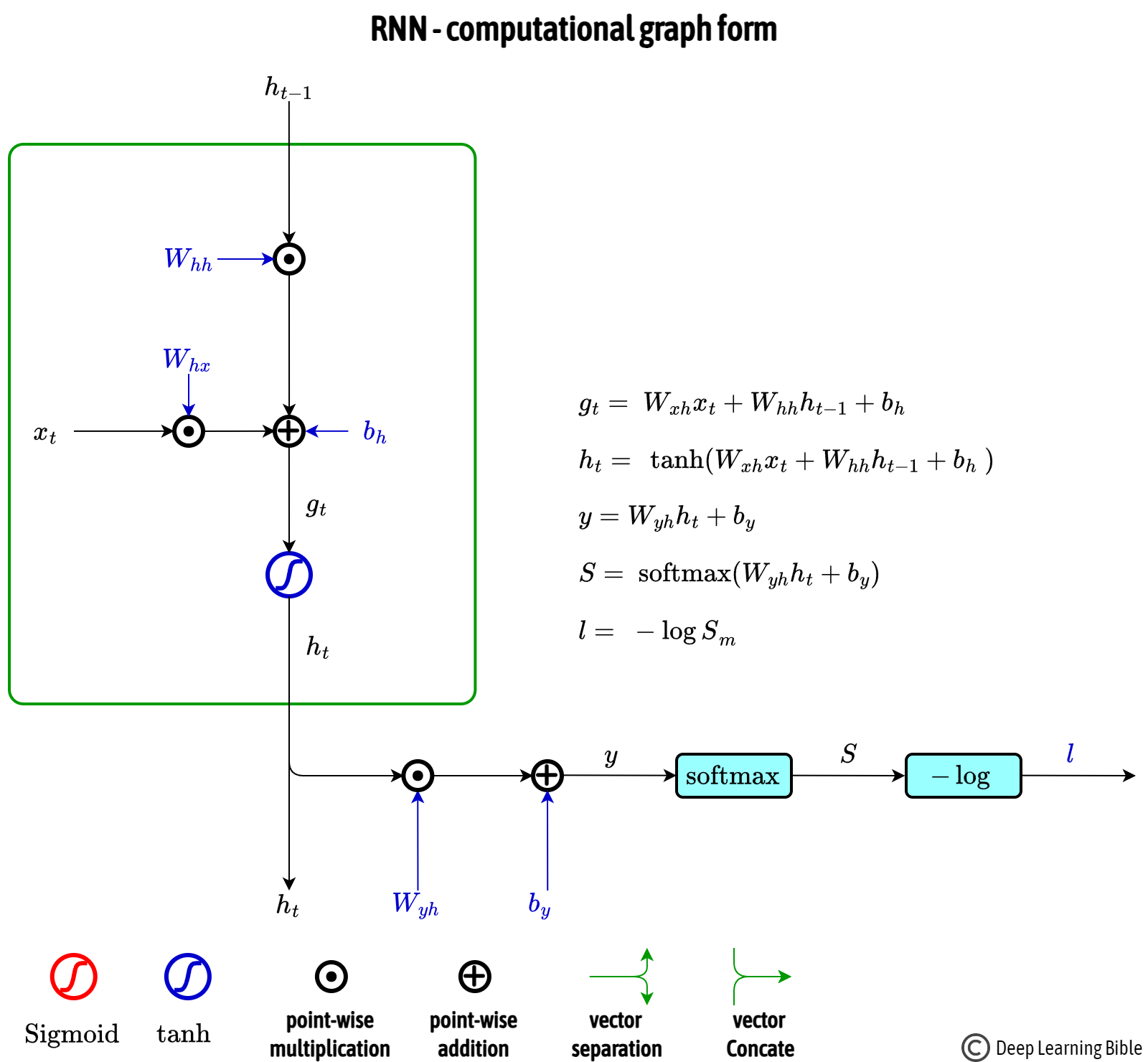
RNN의 핵심 개념은 은닉 상태(Hidden State)이다. 현재 입력값과 이전 시점의 은닉 상태를 이용하여 새로운 은닉 상태를 계산하며, 이를 통해 연속적인 정보를 유지한다.

은닉 상태의 계산

각 시점 $t$에서 RNN의 은닉 상태는 다음과 같이 계산된다.

$$ h_t = \sigma_h(W_{hh} h_{t-1} + W_{xh} x_t + b_h) $$

  • $\sigma_h$ : 순환 신경망의 은닉 상태를 계산하기 위한 활성화 함수
  • $W_{hh}$ : 이전 시점의 은닉 상태 $h_{t-1}$에 대한 가중치
  • $W_{xh}$ : 현재 입력값 $x_t$에 대한 가중치
  • $b_h$ : 은닉 상태 $h_t$의 편향

출력값의 계산

출력값 $ y_t $는 현재 은닉 상태를 이용해 다음과 같이 계산된다.

$$ y_t = \sigma_y(W_{hy} h_t + b_y) $$

  • $\sigma_y$ : 출력값을 계산하기 위한 활성화 함수
  • $W_{hy}$ : 현재 시점의 은닉 상태 $h_t$에 대한 가중치
  • $b_y$ : 출력값 $y_t$의 편향

이처럼 RNN은 과거의 정보를 계속 은닉 상태에 저장하면서 새로운 입력값을 반영하는 방식으로 작동한다.

순환 신경망의 다양한 구조

RNN은 다양한 방식으로 설계될 수 있으며, 크게 일대다(One-to-Many), 다대일(Many-to-One), 다대다(Many-to-Many) 구조가 존재한다.

일대다 구조

하나의 입력에 대해 여러 개의 출력을 생성하는 구조이다. 예를 들어, 이미지 캡셔닝(Image Captioning)에서는 하나의 이미지를 입력받아 여러 단어로 구성된 설명 문장을 출력한다.

다대일 구조

여러 개의 입력을 받아 하나의 출력을 생성하는 구조이다. 감성 분석(Sentiment Analysis)이 대표적인 예로, 한 문장의 감정이 긍정인지 부정인지를 분류하는 작업이다.

다대다 구조

입력과 출력이 모두 시퀀스로 이루어진 구조이다. 예를 들어, 번역 모델(Translation)이나 음성 인식(Speech Recognition)에서 활용된다.

RNN 구현 예제

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18

import torch
import torch.nn as nn

# RNN 모델 정의
model = nn.RNN(input_size=128, hidden_size=256, num_layers=3, batch_first=True, bidirectional=True)

# 입력 데이터 생성
batch_size = 4
sequence_len = 6
inputs = torch.randn(batch_size, sequence_len, 128)
h_0 = torch.rand(6, batch_size, 256)  # (num_layers * bidirectional, batch, hidden_size)

# 순방향 연산
outputs, hidden = model(inputs, h_0)

# 출력 차원 확인
print(outputs.shape)  # torch.Size([4, 6, 512])
print(hidden.shape)   # torch.Size([6, 4, 256])

장단기 메모리

장단기 메모리(Long Short-Term Memory, LSTM)는 순환 신경망(RNN) 기법의 하나로 기존 순환 신경망이 갖고 있던 기억력 부족과 기울기 소실 문제를 방지하도록 개발되었다.

LSTM

RNN의 한계

RNN은 기본적으로 시퀀스를 잘 처리할 수 있는 구조지만, 학습 과정에서 다음과 같은 문제가 발생할 수 있다.

  • 장기 의존성 문제(Long-term dependencies): 과거의 정보를 장기간 유지하기 어렵다.
  • 기울기 소실(Vanishing Gradient) 문제: 역전파 과정에서 기울기가 너무 작아지면서 학습이 어려워진다.

이러한 문제를 해결하기 위해 장단기 메모리 모델이 개발되었다.

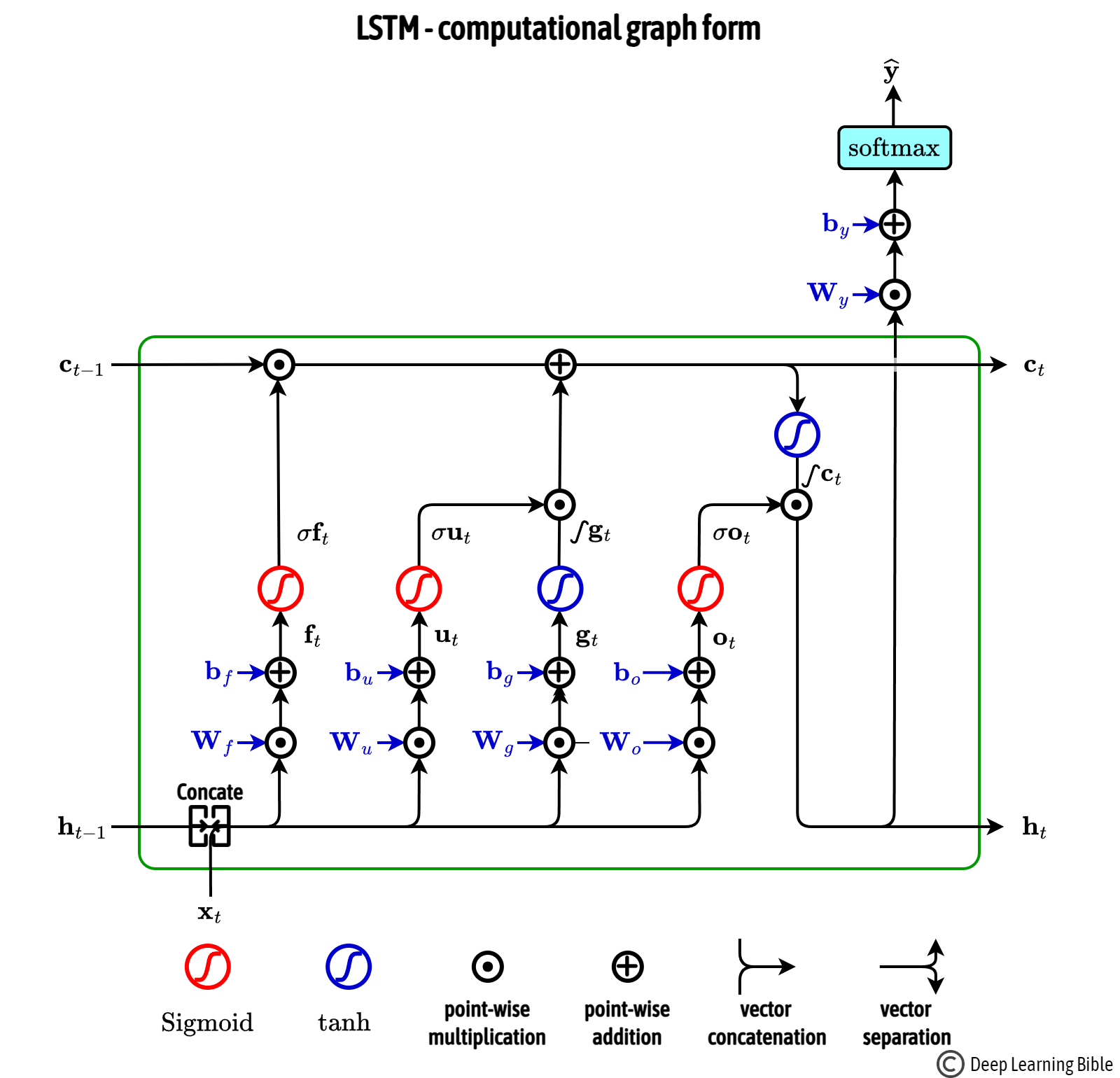
LSTM의 구조

LSTM은 RNN과 유사하지만, 셀 상태(Cell State)와 게이트(Gate) 구조를 추가하여 중요한 정보를 선택적으로 저장하거나 삭제할 수 있도록 설계되었다.

  1. 망각 게이트 $$ f_t = \sigma(W_x^{(f)} x_t + W_h^{(f)} h_{t-1} + b^{(f)}) $$

  2. 기억 게이트 $$ g_i = \tanh(W_x^{(g)} x_t + W_x^{(g)} h_{t-1} + b^{(g)}) $$ $$ i_i = \text{sigmoid}(W_x^{(i)} x_t + W_x^{(i)} h_{t-1} + b^{(i)}) $$

  3. 메모리 셀 계산 $$ C_t = f_t \odot C_{t-1} + i_t \odot g_t $$

  4. 출력 게이트 $$ o_t = \sigma(W_x^{(o)} x_t + W_h^{(o)} h_{t-1} + b^{(o)}) $$

이러한 구조 덕분에 LSTM은 중요한 정보는 오래 기억하면서 불필요한 정보는 쉽게 잊을 수 있어, 장기 의존성 문제를 해결할 수 있다.

LSTM 구현 예제

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

model = nn.LSTM(input_size=128, hidden_size=256, num_layers=3, batch_first=True, bidirectional=True)

inputs = torch.randn(batch_size, sequence_len, 128)
h_0 = torch.rand(6, batch_size, 256)
c_0 = torch.rand(6, batch_size, 256)

outputs, (h_n, c_n) = model(inputs, (h_0, c_0))

print(outputs.shape)  # torch.Size([4, 6, 512])
print(h_n.shape)  # torch.Size([6, 4, 256])
print(c_n.shape)  # torch.Size([6, 4, 256])
© 2021 - 2025 Gyeongmin Lee