단어의 분산 표현

본 포스팅은 ‘밑바닥부터 시작하는 딥러닝 2’ 교재를 참고했습니다.

자연어 처리와 단어의 의미

자연어(Natural Language)란 우리가 평소에 사용하는 언어, 예를 들어 한국어나 영어를 말한다. 자연어 처리(NLP, Natural Language Processing)는 이러한 자연어를 컴퓨터가 이해하도록 만드는 기술 분야이다.

우리의 말은 문자로 이루어져 있고, 말의 의미는 단어로 구성된다. 따라서 컴퓨터가 자연어를 이해하도록 하려면 우선 단어의 의미부터 이해시켜야 한다.

시소러스

단어의 의미를 나타내는 가장 Naive한 방법

사람이 직접 단어의 의미를 정의하는 방식으로, 쉽게 말해 ‘유의어 사전’이다.

car, auto, automobile은 모두 자동차를 나타낸다. 시소러스에서는 이러한 유의어/동의어를 한 그룹으로 분류한다.

graph LR
car~~~auto~~~automobile

또한 단어 간의 상위/하위, 전체/부분 등 세세한 관계까지 정의하기도 한다.

flowchart TD
    a[object] --> b[mortor vehicle]
    b --> d[go-cart]
    b --> c[car]
    b --> e[truck]
    c --> f[suv]
    c --> g[compact]
    c --> h[hatch-back]

WordNet

1985년 구축된 WordNet은 자연어 처리 분야에서 가장 유명한 시소러스이다.

WordNet을 사용하면 유의어를 얻거나, 단어 네트워크를 사용해 단어 간의 유사도를 구할 수 있다.

문제점

사람이 수작업으로 라벨링 해야하기에 여러 단점이 존재한다.

시대 변화에 대응하기 어렵다.
- 단어의 의미는 시간이 지남에 따라 변하기도 하고, 새로운 단어가 생기기도 한다.
비용이 많이 든다.
- 영어 단어만 해도 1000만개가 넘으며, 이는 높은 인적 비용을 요구한다.
단어 간의 미묘한 차이를 표현할 수 없다.
- 예를 들어 빈티지와 레트로의 경우 의미는 같지만, 용법은 다르다. 시소러스는 이러한 차이를 표현할 수 없다.

통계 기반 기법

통계 기반 기법을 사용하기 위해 우리는 말뭉치(corpus)를 이용할 것이다.

말뭉치란 자연어처리 연구나 어플리케이션을 위해 수집된 대량의 텍스트 데이터로, 대표적인 말뭉치는 위키백과, 구글뉴스, 셰익스피어의 소설 등이 있다.

말뭉치 전처리

작은 말뭉치를 전처리하는 과정을 살펴보자.

1
2
3
4
5


>>> text = 'You say goodbye and I say hello.'
>>> text = text.lower()  # 모두 소문자로 변환
>>> text = text.replace('.', ' .')  # '.'을 ' .'으로 변환
>>> text 
'you say goodbye and i say hello .'

모든 단어를 소문자로 변환하고, 단어의 마지막 점을 띄워줬다.

1
2
3


>>> words = text.split()  # 공백을 기준으로 나눔
>>> words 
['you', 'say', 'goodbye', 'and', 'i', 'say', 'hello', '.']

공백을 기준으로 나눠, 리스트에 담았다.

1
2
3
4
5
6
7


>>> word_to_id = {}
>>> id_to_word = {}
>>> for word in words:
...     if word not in word_to_id:
...         new_id = len(word_to_id)
...         word_to_id[word] = new_id
...         id_to_word[new_id] = word

word_to_id 의 경우 key가 단어, value는 id이다. id_to_word는 그 반대이다.

1
2
3
4


>>> id_to_word
{0: 'you', 1: 'say', 2: 'goodbye', 3: 'and', 4: 'i', 5: 'hello', 6: '.'}
>>> word_to_id
{'you': 0, 'say': 1, 'goodbye': 2, 'and': 3, 'i': 4, 'hello': 5, '.': 6}

마지막으로 단어 목록을 단어 ID 목록으로 변환하면 된다.

1
2
3
4


>>> import numpy as np
>>> corpus = np.array([word_to_id[w] for w in words])
>>> corpus
array([0, 1, 2, 3, 4, 1, 5, 6])

이렇게 범주형 변수를 숫자로 바꾸는 것을 원 핫 인코딩(one-hot encodeing) 이라고 한다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


def preprocess(text):
    text = text.lower()
    text = text.replace('.', ' .')
    words = text.split(' ')

    word_to_id = {}
    id_to_word = {}
    for word in words:
        if word not in word_to_id:
            new_id = len(word_to_id)
            word_to_id[word] = new_id
            id_to_word[new_id] = word

    corpus = np.array([word_to_id[w] for w in words])

    return corpus, word_to_id, id_to_word

위 과정을 합쳐 단어를 전처리하는 preprocess 함수를 구현했다.

분포 가설과 분산 표현

비슷한 위치에서 등장한 단어는 비슷한 의미를 가지지 않을까?

“단어의 의미는 주변 단어에 의해 형성된다.” 라는 것을 분포 가설이라고 한다.

단어 자체에는 의미가 없고, 그 단어가 사용 된 맥락이 의미를 형성한다는 것이다. 여기서 맥락이란 특정 단어를 중심에 둔 그 주변 단어를 말한다.

좌우 모든 단어를 고려하며 계산하면 컴퓨팅 비용이 너무 많이 들기에, 우리는 특정 크기만큼만 고려할 것이다. 즉, 슬라이딩 윈도우를 적용할 것이다. ‘맥락의 크기’는 슬라이딩 윈도우의 사이즈와 같다.

분산 표현 이란 분포 가설에 기반해 주변 단어의 분포를 기준으로 단어의 벡터 표현을 결정하는 것 이다.

동시 행렬 발생

분포 가설에 기초해 단어를 벡터로 나타내 보자.

가장 간단한 방법은 한 단어에 주목하여, 주변에 어떤 단어가 몇 번 등장했는지 계산하는 것이다. 이는 통계 기반 기법(statistical based)이라고 한다.

{‘you’: 0, ‘say’: 1, ‘goodbye’: 2, ‘and’: 3, ‘i’: 4, ‘hello’: 5, ‘.’: 6}

예를 들어, ‘you say goodbye and i say hello .’ 에서 ‘say’를 기준으로 살펴보자.

‘say’ 좌우로 ‘you’, ‘goodbye’, ‘i’, ‘hello’ 가 있다.

이는 벡터 ‘[1, 0, 1, 0, 1, 1, 0]’ 으로 표현 할 수 있을 것이다.

이것을 모든 단어에 대해 적용시킨다면 아래와 같은 테이블을 얻을 수 있을 것이다.

	you	say	goodbye	and	i	hello	.
you	0	1	0	0	0	0	0
say	1	0	1	0	1	1	0
goodbye	0	1	0	1	0	0	0
and	0	0	1	0	1	0	0
i	0	1	0	1	0	0	0
hello	0	1	0	0	0	0	1
.	0	0	0	0	0	1	0

이것을 동시 발생 행렬 이라고 한다.

동시 발생 행렬을 만드는 코드는 아래와 같다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


def create_co_matrix(corpus, vocab_size, window_size=1):
    corpus_size = len(corpus)
    co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)

    for idx, word_id in enumerate(corpus):
        for i in range(1, window_size + 1):
            left_idx = idx - i
            right_idx = idx + i

            if left_idx >= 0:
                left_word_id = corpus[left_idx]
                co_matrix[word_id, left_word_id] += 1
            if right_idx < corpus_size:
                right_word_id = corpus[right_idx]
                co_matrix[word_id, right_word_id] += 1
    return co_matrix

벡터간 유사도

앞서 구한 행렬을 통해 벡터 간의 유사도를 구한다면 단어 간의 유사도를 구할 수 있을 것이다.

벡터의 유사도를 측정하는 대표적인 방법으로는 벡터의 내적이나 유클리드 거리, 코사인 유사도가 있다. 이 중, 우리는 코사인 유사도를 사용할 것이다.

$$ \tag{1} \text{similarity}(A, B)=\frac{A⋅B}{||A||\ ||B||}=\frac{\sum_{i=1}^{n}{A_{i}B_{i}}}{\sqrt{\sum_{i=1}^{n}(A_{i})^2}\sqrt{\sum_{i=1}^{n}(B_{i})^2}} $$

[식 1]의 분자에는 벡터의 내적이, 분모에는 각 벡터의 노름(norm)이 등장한다. 노름은 벡터의 크기를 나타낸 것으로, 여기선 L2 노름을 계산한다.

코사인 유사도는 두 벡터가 가르키는 방향이 얼마나 유사한지를 나타낸다. 방향이 같으면 1, 반대면 -1이다.

파이썬 코드로는 아래와 같이 나타낼 수 있다.

1
2
3
4


def cos_similarity(x, y, eps=1e-8):
    nx = x / (np.sqrt(np.sum(x ** 2)) + eps)  # x의 정규화
    ny = y / (np.sqrt(np.sum(y ** 2)) + eps)  # y의 정규화
    return np.dot(nx, ny)

0으로 나누어 오류가 나는 일이 없도록 $10^{-8}$ 이라는 작은 값을 더해주는 것을 볼 수 있다.

유사 단어의 랭킹

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24


def most_similar(query, word_to_id, id_to_word, word_matrix, top=5):
    if query not in word_to_id:
        print('%s is not found' % query)
        return

    print('\n[query] ' + query)
    query_id = word_to_id[query]
    query_vec = word_matrix[query_id]

    vocab_size = len(id_to_word)

    similarity = np.zeros(vocab_size)
    for i in range(vocab_size):
        similarity[i] = cos_similarity(word_matrix[i], query_vec)

    count = 0
    for i in (-1 * similarity).argsort():
        if id_to_word[i] == query:
            continue
        print(' %s: %s' % (id_to_word[i], similarity[i]))

        count += 1
        if count >= top:
            return

위 코드로 ‘you’ 와 유사한 단어를 찾아보자.

	Value
goodbye	0.7071067691154799
i	0.7071067691154799
hello	0.7071067691154799
say	0.0
and	0.0

‘goodbye’, ‘i’, ‘hello’의 경우 ‘say’나 ‘and’에 비해 유사하다고 볼 수 있다.

통계 기반 기법의 개선

상호정보량

발생 횟수는 좋은 특징이 아니다

동시 발생 행렬은 두 단어가 동시에 발생한 빈도를 측정한다. 하지만 이것만으로는 부족하다. ’the’, ’this’처럼 고빈도 단어 의 경우를 생각해 보자.

‘drive’, ’the’ 중에 ‘car’와 더 유사한 단어는 무엇인가? 모두 ‘drive’와 유사한 단어로 ‘car’를 고를 것이다.

하지만 동시 발생 빈도는 ’the’가 압도적으로 높을 것이다. 동시 발생 행렬에서는 ’the’ 자체가 문서에서 더 많이 등장하기에, 더 높은 유사성을 갖는다고 잘못 평가할 수 있다.

이 문제를 해결하기 위해 점별 상호정보량(PMI, Pointwise Mutual Information) 이라는 척도를 사용할 것이다.

PMI는 확률 변수 $x$와 $y$에 대해 다음과 같은 식으로 정의된다.

$$ \tag{2} \text{PMI}(x,y)=\log_2\frac{P(x,y)}{P(x)P(y)} $$

[식 2]에서 $P(x)$는 $x$가 일어날 확률, $P(y)$는 $y$가 일어날 확률, $P(x,y)$는 $x, y$가 동시에 일어날 확률이다. PMI가 높을 수록 관련성이 높다는 의미이다.

자연어 처리에서 $P(x)$는 말뭉치에서 $x$라는 단어가 등장할 확률이다. 예를 들어, 단어 100,000개의 말뭉치에서 ’the’라는 단어가 100번 등장했다면, $P(`\text{the}’) = 0.0001$이다.

하지만 PMI도 문제가 있다. 동시 발생 횟수가 0이라면 PMI 값은 $-\infty$가 된다.

따라서 PPMI(Positive PMI) 라는 척도를 쓴다. 이는 다음과 같다.

$$ \tag{3} \text{PPMI}(x, y) = \max(0, \text{PMI}(x,y)) $$

[식 3]을 보면, PPMI는 PMI값이 음수면 0으로 취급한다는 것을 확인할 수 있다.

이제 PPMI를 파이썬으로 구현해 보자.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11


def ppmi(C, eps = 1e-8):
    M = np.zeros_like(C, dtype=np.float32)
    N = np.sum(C)
    S = np.sum(C, axis=0)

    for i in range(C.shape[0]):
        for j in range(C.shape[1]):
            pmi = np.log2(C[i, j] * N / (S[j]*S[i]) + eps)
            M[i, j] = max(0, pmi)

    return M

이제 동시 발생 행렬을 PPMI로 변환해 보자.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12


text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)
W = ppmi(C)

np.set_printoptions(precision=3)  # 유효 자릿수를 세 자리로 표시
print('동시발생 행렬')
print(C)
print('-'*50)
print('PPMI')
print(W)

위 코드를 실행시킨 결과는 아래와 같다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


동시발생 행렬
[[0 1 0 0 0 0 0]
 [1 0 1 0 1 1 0]
 [0 1 0 1 0 0 0]
 [0 0 1 0 1 0 0]
 [0 1 0 1 0 0 0]
 [0 1 0 0 0 0 1]
 [0 0 0 0 0 1 0]]
--------------------------------------------------
PPMI
[[0.    1.807 0.    0.    0.    0.    0.   ]
 [1.807 0.    0.807 0.    0.807 0.807 0.   ]
 [0.    0.807 0.    1.807 0.    0.    0.   ]
 [0.    0.    1.807 0.    1.807 0.    0.   ]
 [0.    0.807 0.    1.807 0.    0.    0.   ]
 [0.    0.807 0.    0.    0.    0.    2.807]
 [0.    0.    0.    0.    0.    2.807 0.   ]]

이제 더 좋은 단어 벡터를 얻었다.

하지만 아직 문제점이 있다. 벡터의 크기가 너무 크다는 것이다. 단어의 개수가 10만개라면, 벡터의 차운 수도 10만이 된다.

또한, 대부분 0으로 구성된 희소행렬(Sparse Matrix)이다.

이는 매우 비효율적이고, 노이즈에 취약하다.

차원 축소

차원 축소는 중요한 정보는 최대한 유지하되, 벡터의 차원을 줄이는 것이다. 그 중 특잇값 분해를 적용해보자.

특잇값 분해에 대한 자세한 설명은 여기 블로그를 참고하자.

특잇값 분해를 사용한 파이썬 코드는 아래와 같다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(id_to_word)
C = create_co_matrix(corpus, vocab_size, window_size=1)
W = ppmi(C)

U, S, V = np.linalg.svd(W)

np.set_printoptions(precision=3)
print(C[0])
print(W[0])
print(U[0])

for word, word_id in word_to_id.items():
    plt.annotate(word, (U[word_id, 0], U[word_id, 1]))
plt.scatter(U[:,0], U[:,1], alpha=0.5)
plt.show()

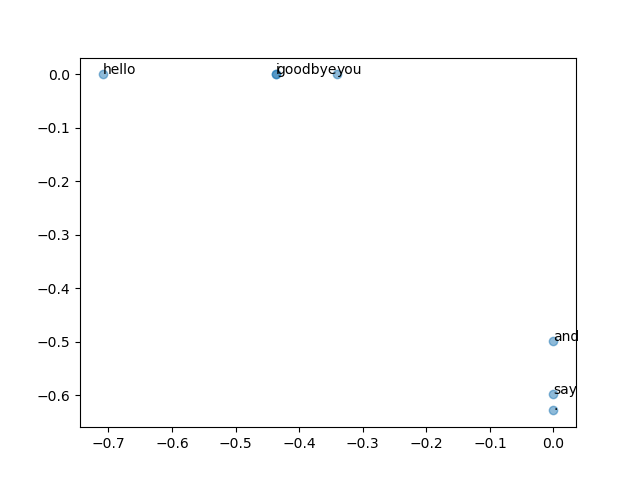
위 코드는 동시발생 행렬에 SVD를 적용한 후 각 단어를 2차원 벡터로 변환한 것을 시각화 한 것이다.

PTB 데이터셋 평가

이번에는 많은 양의 데이터를 처리해야 하므로, sklearn의 고속 SVD를 사용하자.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


from dataset import ptb
from sklearn.utils.extmath import randomized_svd

window_size = 2
wordvec_size = 100

corpus, word_to_id, id_to_word = ptb.load_data('train')
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size, window_size)
W = ppmi(C, verbose=True)

U, S, V = randomized_svd(W, n_components=wordvec_size, n_iter=5)

word_vecs = U[:, :wordvec_size]

querys = ['you', 'year', 'car', 'toyota']
for query in querys:
    most_similar(query, word_to_id, id_to_word, word_vecs, top=5)

이제 드디어 단어의 의미를 벡터로 잘 인코딩했다.

말뭉치를 사용해 맥락에 속한 단어의 등장 횟수를 센 후 PPMI 행렬로 변환하고, 다시 SVD를 이용해 차원을 감소시킴으로써 더 좋은 단어 벡터를 얻어냈다.

이것이 단어의 분산 표현이고, 각 단어는 고정 길이의 밀집벡터로 표현되었다.

단어의 벡터 공간에서는 의미가 가까운 단어는 그 거리도 가깝다.