word2vec을 이용한 단어 임베딩

본 포스팅은 ‘밑바닥부터 시작하는 딥러닝 2’ 교재를 참고했습니다.

추론 기반 기법과 신경망

단어를 벡터로 표현하는 방법은 통계 기반 기법과 추론 기반 기법이 있다. 둘 모두 분포 가설을 기반으로 한다.

통계 기반 기법의 문제점

통계 기반 기법은 주변 단어의 빈도를 기초로 단어를 표현한다. 단어 수가 $N$개일 때, $N \times N$이라는 거대한 행렬을 만들게 된다. 영어 어휘만 해도 100만 개에 가까운데, 그렇다면 1조개의 원소를 가진 행렬이 필요하다는 것이다.

이렇게 통계 기반 기법처럼 학습 데이터를 한번에 처리하지 말고, 데이터를 작게 나눠 순차적으로 학습시키는 (미니배치 학습) 방법이 필요하다.

추론 기반 기법의 개요

추론이란 주변 단어 (맥락)가 주어졌을 때, 무슨 단어가 들어갈 지 단어를 유추하는 것이다.

맥락 정보를 입력받아 출현할 수 있는 단어들의 확률분포를 나타내는 모델을 만들고, 학습의 결과로 분산 표현을 얻는 것이 추론 기반 기법이다.

신경망에서의 단어 처리

신경망은 단어를 그대로 처리할 수 없기 때문에, 단어를 고정된 길이의 벡터로 변환해야 한다. 이를 위해 가장 대표적으로 사용되는 방법이 원핫 인코딩(one-hot encoding)이다.

단어(텍스트)	단어 ID	원핫 표현
you	0	(1, 0, 0, 0, 0, 0, 0, 0)
goodbye	2	(0, 0, 1, 0, 0, 0, 0, 0)

위와 같이 단어는 텍스트, 단어 ID, 원핫 표현으로 나타낼 수 있다. 단어를 고정 크기의 원핫 표현으로 나타내게 되면 뉴런의 수를 고정할 수 있다.

신경망을 구성하는 계층들이 벡터를 처리할 수 있으므로, 이제 단어를 신경망으로 처리할 수 있을 것이다.

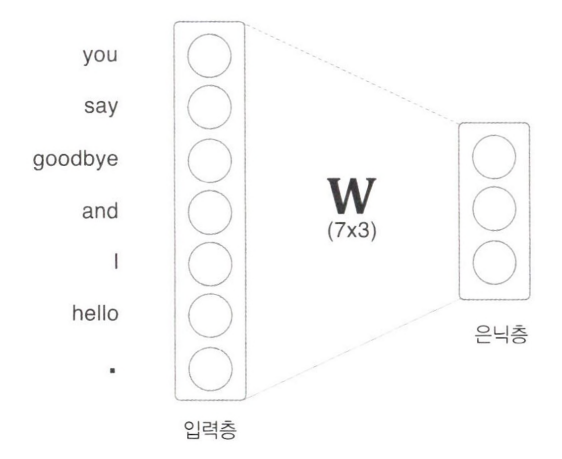
완전연결계층에 의한 변환을 단순화한 그림

완전연결계층의 계산은 행렬 곱으로 수행할 수 있고. 행렬 곱은 넘파이의 np.matmul()로 할 수 있다.

CBOW

CBOW 모델의 추론 처리

CBOW 모델은 맥락으로부터 타깃을 추측하는 용도의 신경망이다. (타깃은 중앙 단어, 맥락은 주변 단어를 의미한다)

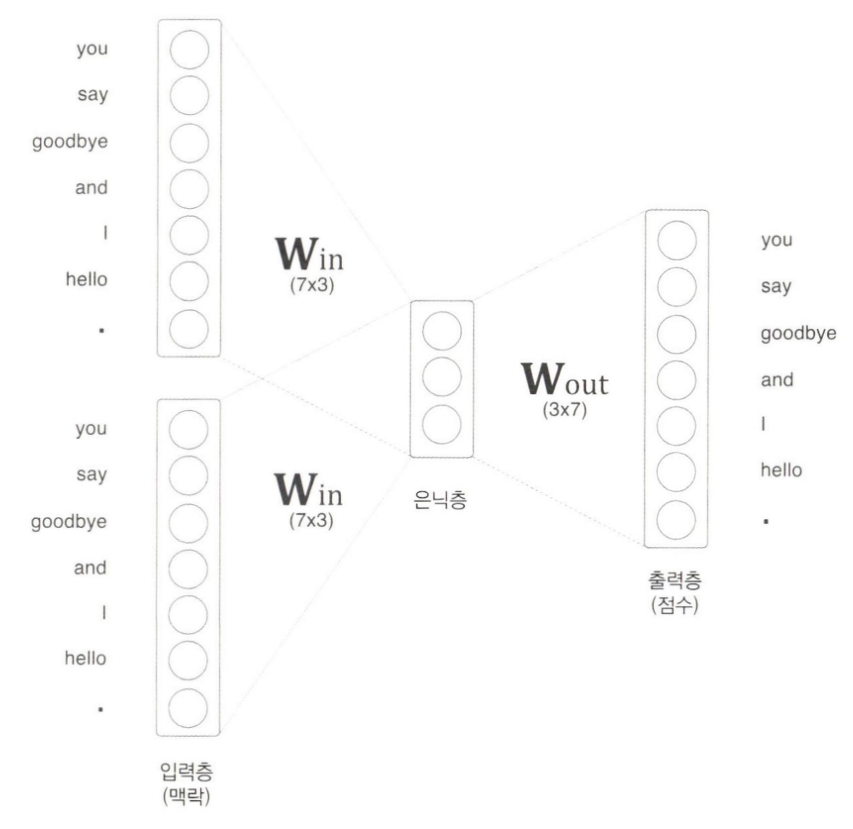
CBOW 모델의 신경망 구조

입력층이 2개 있고, 은닉층을 거쳐 출력층에 도달한다.

두 입력층에서 은닉층으로의 변환은 완전연결계층이 수행한다. 그리고 은닉층에서 출력층 뉴런으로의 변환은 다른 완전연결계층이 처리한다. 입력층이 여러 개이면 전체를 평균하면 된다.

출력층의 뉴런은 총 7개인데, 이 뉴런 하나하나가 각각의 단어에 대응한다. 출력층 뉴런은 각 단어의 점수를 뜻하며, 값이 높을수록 대응 단어의 출현 확률도 높아진다. 이 점수에 소프트맥스 함수를 적용해서, 확률을 얻을 수 있다.

학습을 진행할수록 맥락에서 출현하는 단어를 잘 추측하는 방향으로 이 분산 표현들이 갱신된다. 이렇게 얻은 벡터에는 단어의 의미도 포함되어 있다.

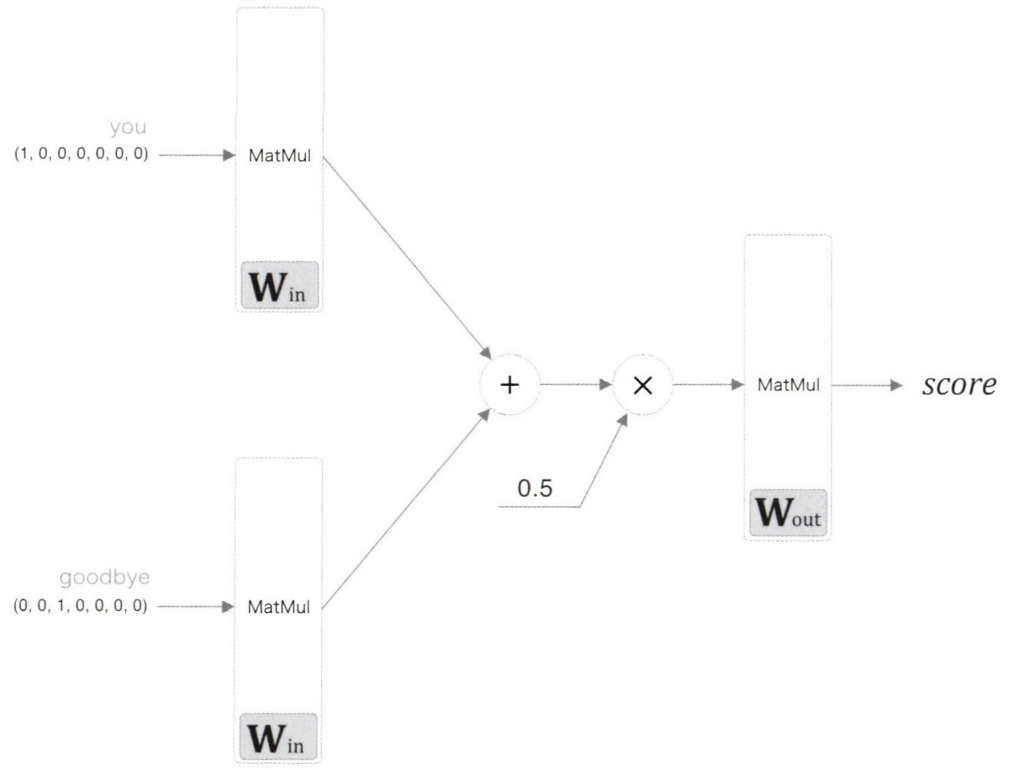
계층 관점에서 본 CBOW 모델의 신경망 구성

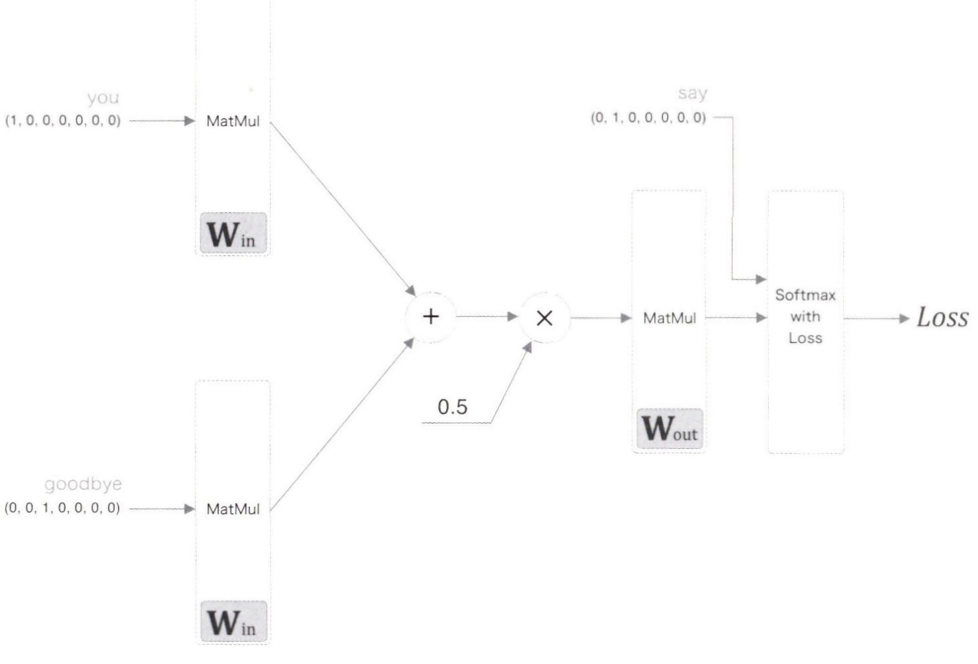
이제 CBOW 모델의 추론 처리를 파이썬으로 구현해 보자.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18


class MatMul:
    def __init__(self, W):
        self.params = [W]
        self.grads = [np.zeros_like(W)]
        self.x = None

    def forward(self, x):
        W, = self.params
        out = np.dot(x, W)
        self.x = x
        return out

    def backward(self, dout):
        W, = self.params
        dx = np.dot(dout, W.T)
        dW = np.dot(self.x.T, dout)
        self.grads[0][...] = dW
        return dx

MatMul 계층은 내부에서 행렬 곱을 계산한다.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19


# 샘플 맥락 데이터
c0 = np.array([[1, 0, 0, 0, 0, 0, 0]])
c1 = np.array([[0, 0, 1, 0, 0, 0, 0]])

# 가중치 초기화
W_in = np.random.randn(7, 3)
W_out = np.random.randn(3, 7)

# 계층 생성
in_layer0 = MatMul(W_in)
in_layer1 = MatMul(W_in)
out_layer = MatMul(W_out)

# 순전파
h0 = in_layer0.forward(c0)
h1 = in_layer1.forward(c1)
h = 0.5 * (h0 + h1)
s = out_layer.forward(h)
print(s)

CBOW 모델은 활성화 함수를 사용하지 않는 간단한 구성의 신경망이다.

CBOW 모델의 학습

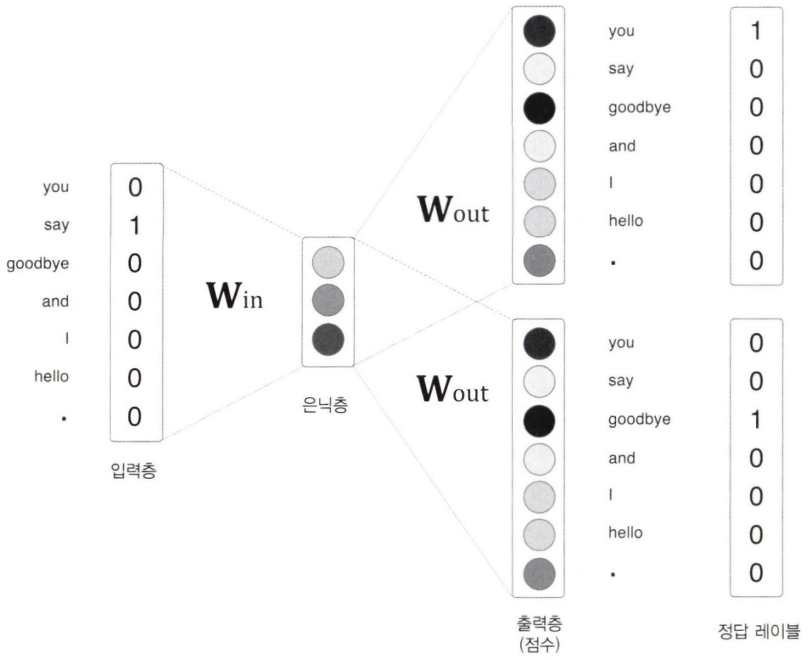
모델이 올바른 예측을 할 수 있도록 가중치를 조정해야 한다.

소프트맥스 함수를 이용 해 점수를 확률로 변환하고, 그 확률과 정답 레이블로부터 교차 엔트로피 오차를 구한 후, 그 값을 손실로 사용해 학습을 진행한다.

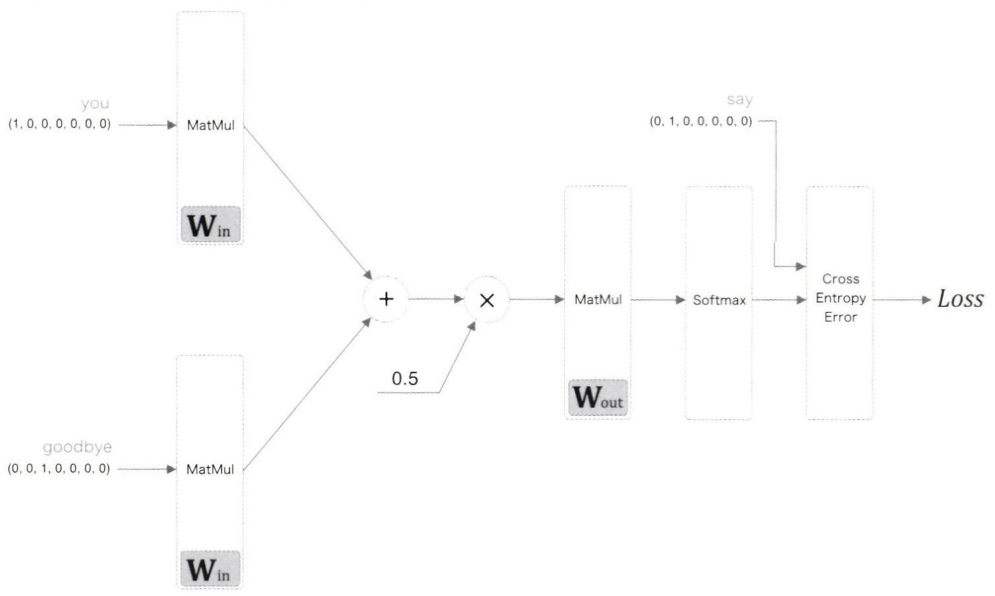
CBOW 모델의 학습 시 신경망 구성

앞서 구현한 추론 처리를 수행하는 CBOW 모델에 Softmax 계층과 Cross Entropy Error 계층을 추가하기만 하면 된다.

word2vec의 가중치와 분산 표현

word2vec에서 사용되는 신경망에는 두 가지 가중치가 존재한다.

입력 측 가중치 $ W_\text{in} $: 입력 측 완전연결계층의 가중치로, 각 행은 해당 단어의 분산 표현을 나타낸다.
출력 측 가중치 $ W_\text{out} $: 출력 측 완전연결계층의 가중치로, 단어의 의미가 인코딩된 벡터가 각 열에 저장된다.

일반적으로 word2vec에서는 입력 측 가중치 $ W_\text{in} $만을 최종 단어의 분산 표현으로 사용한다. 출력 측 가중치는 대부분의 연구에서 버려진다.

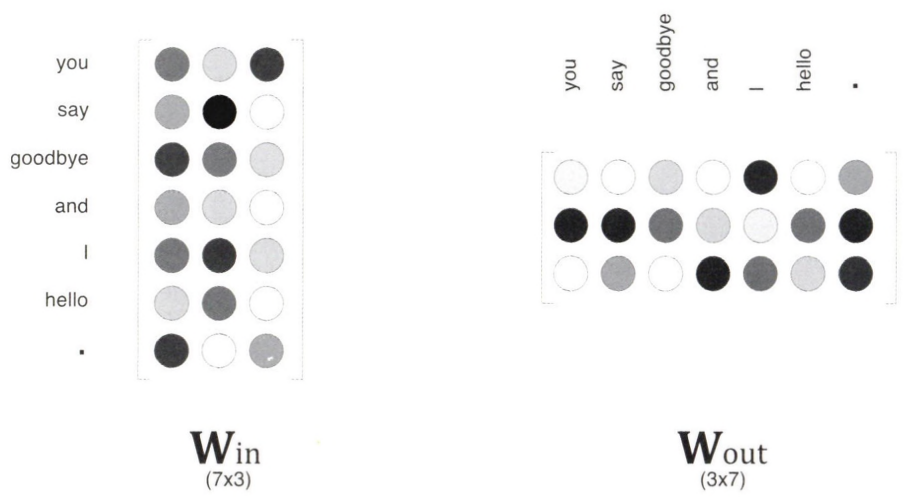
각 단어의 분산 표현

두 가중치는 하나만 이용할 수도 있고, 둘을 합쳐서 사용할 수도 있다.

word2vec의 skip-gram 등 많은 연구에서는 입력 측의 가중치만 사용하고, GloVe에서는 두 가중치를 더하여 사용한다.

학습 데이터 준비

“You say goodbye and I say hello” 문장을 이용해 학습을 진행해 보자.

문장을 전처리하는 preprocess 함수는 여기를 참고하자.

맥락과 타깃

word2vec에서 이용하는 신경망의 입력은 맥락이다. 그 정답 레이블은 중앙 단어인 타깃 이다. 우리는 맥락을 입력했을 때, 타깃을 출력할 확률이 높아지도록 학습시키면 된다.

맥락과 타깃의 예시

맥락과 타깃을 만드는 함수를 구현해 보자.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13


def create_contexts_target(corpus, window_size=1):
    target = corpus[window_size:-window_size]
    contexts = []

    for idx in range(window_size, len(corpus)-window_size):
        cs = []
        for t in range(-window_size, window_size + 1):
            if t == 0:
                continue
            cs.append(corpus[idx + t])
        contexts.append(cs)

    return np.array(contexts), np.array(target)

원핫 벡터로 변환

맥락과 타깃을 단어 ID에서 원핫 표현으로 변환하기 위해, 원핫 벡터로 변환하는 함수를 구현해 보자.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16


def convert_one_hot(corpus, vocab_size):
    N = corpus.shape[0]

    if corpus.ndim == 1:
        one_hot = np.zeros((N, vocab_size), dtype=np.int32)
        for idx, word_id in enumerate(corpus):
            one_hot[idx, word_id] = 1

    elif corpus.ndim == 2:
        C = corpus.shape[1]
        one_hot = np.zeros((N, C, vocab_size), dtype=np.int32)
        for idx_0, word_ids in enumerate(corpus):
            for idx_1, word_id in enumerate(word_ids):
                one_hot[idx_0, idx_1, word_id] = 1

    return one_hot

CBOW 모델 구현

그럼 이제 모델을 구현해 보자.

CBOW 모델의신경망 구성

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39


class SimpleCBOW:
    def __init__(self, vocab_size, hidden_size):
        V, H = vocab_size, hidden_size

        # 가중치 초기화
        W_in = 0.01 * np.random.randn(V, H).astype('f')
        W_out = 0.01 * np.random.randn(H, V).astype('f')

        # 계층 생성
        self.in_layer0 = MatMul(W_in)
        self.in_layer1 = MatMul(W_in)
        self.out_layer = MatMul(W_out)
        self.loss_layer = SoftmaxWithLoss()

        # 모든 가중치와 기울기를 리스트에 모은다.
        layers = [self.in_layer0, self.in_layer1, self.out_layer]
        self.params, self.grads = [], []
        for layer in layers:
            self.params += layer.params
            self.grads += layer.grads

        # 인스턴스 변수에 단어의 분산 표현을 저장한다.
        self.word_vecs = W_in

    def forward(self, contexts, target):
        h0 = self.in_layer0.forward(contexts[:, 0])
        h1 = self.in_layer1.forward(contexts[:, 1])
        h = (h0 + h1) * 0.5
        score = self.out_layer.forward(h)
        loss = self.loss_layer.forward(score, target)
        return loss

    def backward(self, dout=1):
        ds = self.loss_layer.backward(dout)
        da = self.out_layer.backward(ds)
        da *= 0.5
        self.in_layer1.backward(da)
        self.in_layer0.backward(da)
        return None

학습코드구현

학습 데이터를 준비해 신경망에 입력한 다음, 기울기를 구하고 가중치 매개변수를 순서대로 갱신해보자.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23


window_size = 1
hidden_size = 5
batch_size = 3
max_epoch = 1000

text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)

vocab_size = len(word_to_id)
contexts, target = create_contexts_target(corpus, window_size)
target = convert_one_hot(target, vocab_size)
contexts = convert_one_hot(contexts, vocab_size)

model = SimpleCBOW(vocab_size, hidden_size)
optimizer = Adam()
trainer = Trainer(model, optimizer)

trainer.fit(contexts, target, max_epoch, batch_size)
trainer.plot()

word_vecs = model.word_vecs
for word_id, word in id_to_word.items():
    print(word, word_vecs[word_id])

Optimizer는 Adam을 사용해서 학습시켰다.

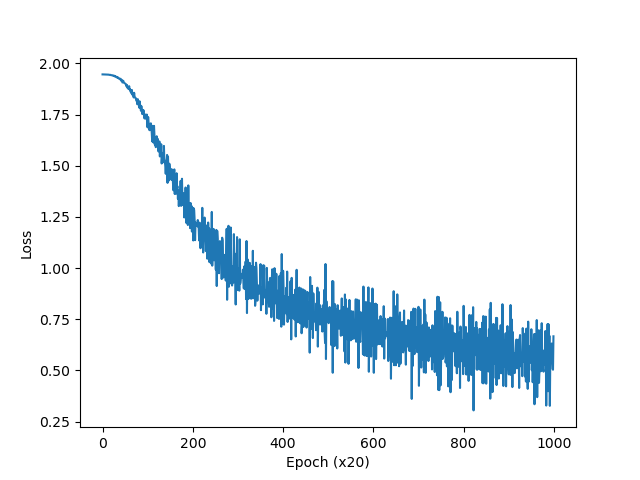
학습 경과 그래프

학습을 거듭할수록 손실이 줄어들고 있다. 그럼 이제 학습이 끝난 후의 가중치 매개변수를 확인해 보자.

1
2
3
4
5
6
7


you [ 1.001226   1.0100921 -1.0480953 -1.1371888  1.4559563]
say [-1.1566567  -1.176362    1.1436371   1.10196     0.29608265]
goodbye [ 0.93248147  0.8733082  -0.8807387  -0.79100204  0.47581592]
and [-0.77025014 -0.7765116   0.7260802   0.86010003  1.9209603 ]
i [ 0.9177614   0.86838746 -0.8880995  -0.7853987   0.48234403]
hello [ 0.97636664  1.0043367  -1.0315654  -1.1388433   1.4567573 ]
. [-1.2583737 -1.2487313  1.2197953  1.20546   -1.6672388]

이제 드디어 단어를 밀집벡터로 나타낼 수 있게 되었다. 이 밀집 벡터가 바로 단어의 분산 표현이다.

학습이 잘 이루어졌으니, 이 분산 표현은 단어의 실제 의미를 담고 있을 것이다.

여태 구현한 CBOW 모델은 처리 효율 면에서 문제가 있다. 이제 그걸 개선해 보자.

word2vec 보충

CBOW 모델과 확률

사건 A가 일어날 확률은 $P(A)$와 같이 표기하고, A와 B가 동시에 일어날 확률은 $P(A, B)$와 같이 표기한다. 사건 B가 일어났을 때 사건 A가 일어날 확률은 $P(A|B)$와 같이 표기한다.

맥락으로 $w_{t-1}$과 $w_{t+1}$ 이 주어졌을 때 $w_t$가 일어날 확률은

$$ P(w_t | w_{t-1}, w_{t+1}) \tag 1 $$

식 1과 같이 쓸 수 있다. 이는 CBOW를 모델링 하는 식이다.

교차 엔트로피 오차 식은 $L = - \sum_k t_k \log y_k$이다. $y_k$는 $k$번째에 해당하는 사건이 일어날 확률을 의미하고, $t_k$는 정답 레이블로 원핫 벡터로 표현된다. 여기서 문제의 정답은 $w_i$가 발생하는 것이므로 $w_i$에 해당하는 원소만 1이고 나머지는 0이 된다. 이 점을 활용하여, 다음 식을 유도할 수 있다.

$$ L = - \log P(w_t \ | \ w_{t-1}, \ w_{t+1}) \tag 2 $$

식 2는 음의 로그 가능도라고 부른다. 이처럼 CBOW 모델의 손실 함수는 식 1의 확률에 $\log$를 취한 다음 마이너스를 붙인 것이다. 이는 샘플 데이터 하나에 대한 손실 함수이고, 이를 corpus 전체로 확장시키면 아래 식 3과 같다.

$$ L = - \frac{1}{T} \sum_{t=1}^T \log P(w_t \ | \ w_{t-1}, \ w_{t+1}) \tag 3 $$

CBOW 모델의 학습이 수행하는 일은 이 손실 함수의 값을 가능한 한 작게 만드는 것이다.

skip-gram 모델

skip-gram은 CBOW에서 다루는 맥락과 타깃을 역전시킨 모델이다.

CBOW 모델과 skip-gram 모델이 다루는 문제

CBOW 모델은 맥락이 여러 개 있고, 그 여러 맥락으로부터 타깃을 추측한다. 반면에 skip-gmm 모델은 중앙의 타깃으로부터 주변의 맥락을 추측한다.

skip-gram 모델의 신경망 구성 예

skip-gram 모델을 확률 표기로 나타내면 아래 식 4와 같다.

$$ P(w_{t-1}, \ w_{t+1} \ | \ w_t) \tag 4 $$

조건부 독립이라고 가정하고 (맥락의 단어 사이에 관련성이 없다고 가정하고) 식 4를 아래 식 5와 같이 분해한다.

$$ P(w_{t-1}, \ w_{t+1} \ | \ w_t) = P(w_{t-1} \ | \ w_{t}) \ P(w_{t+1} \ | \ w_{t}) \tag 5 $$

위 식을 교차 엔트로피 오차에 적용하고, corpus 전체로 확장시키면 아래 식 6이 된다.

$$ L = - \frac{1}{T} \sum_{t=1}^T ( \log P(w_{t-1} \ | \ w_{t})+ P(w_{t+1} \ | \ w_{t})) \tag 6 $$

skip-gram 모델은 맥락의 수만큼 추측하기 때문에 그 손실 함수는 각 맥락에서 구한 손실의 총합이어야 하는 반면, CBOW 모델은 타깃 하나의 손실을 구한다.

단어 분산 표현의 정밀도 면에서 skip-gram 모델의 결과가 더 좋은 경우가 많고, corpus가 클 수록 성능 면에서 skip-gram이 뛰어난 경향이 있다.

통계 기반 vs 추론 기반

통계 기반 기법과 추론 기반 기법인 word2vec은 학습과 갱신 방식에서 차이를 보인다.

통계 기반은 새 단어 추가 시 처음부터 다시 계산해야 하지만, word2vec은 기존 가중치를 활용해 효율적으로 갱신할 수 있다. 단어의 유사성과 복잡한 패턴 인코딩에서도 word2vec이 더 복잡한 관계를 파악할 수 있으며, ‘king - man + woman = queen’ 같은 유추 문제를 풀 수 있다.

그러나 실제 유사성 평가에서는 두 기법 간 우열을 가리기 어렵다. 추론 기반과 통계 기반은 서로 관련되어 있으며, 이를 바탕으로 추론 기반과 통계 기반을 융합한 GloVe 기법이 등장하여 두 방법의 장점을 결합했다.